题目内容
 选修4-1:几何证明选讲
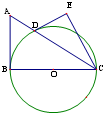
选修4-1:几何证明选讲如图,已知AB切圆O于点B,BC是圆O的直径,AC交圆O于点D,DE是圆O的切线,CE⊥DE于E,DE=3,CE=4,求AB的长.
考点:与圆有关的比例线段
专题:立体几何
分析:连接OD,可得OD∥CE,进而∠ECD=∠ODC=∠OCD,结合DE=3,CE=4,先后求出CD,OC,进而可得AB的长.
解答:
解:连接OD,

∵DE是圆O的切线,
∴OD⊥DE,
又∵CE⊥DE于E,
∴OD∥CE,
∴∠ECD=∠ODC=∠OCD,
∵DE=3,CE=4,
∴CD=5,
∴tan∠ECD=tan∠ODC=tan∠OCD=
,
∴cos∠OCD=
,
故OC=
=
,
∴BC=2OC=
,
故AB=BC•tan∠OCD=

∵DE是圆O的切线,
∴OD⊥DE,
又∵CE⊥DE于E,
∴OD∥CE,
∴∠ECD=∠ODC=∠OCD,
∵DE=3,CE=4,
∴CD=5,
∴tan∠ECD=tan∠ODC=tan∠OCD=
| 3 |
| 4 |
∴cos∠OCD=
| 4 |
| 5 |
故OC=
| ||
| cos∠OCD |
| 25 |
| 8 |
∴BC=2OC=
| 25 |
| 4 |
故AB=BC•tan∠OCD=
| 75 |
| 16 |
点评:本题考查的知识点是切线的性质,解直角三角形,是三角函数与切线性质的综合应用,难度中档.

练习册系列答案
相关题目
在△ABC中,若|
+
|=|
-
|,AB=2,AC=1,E,F为BC边的三等分点,则
•
=( )
| AB |
| AC |
| AB |
| AC |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已f(x)=2sin(
x+
),f(x)的最小正周期是( )
| π |
| 2 |
| π |
| 3 |
| A、2 | B、4π | C、2π | D、4 |
 如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为
如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为