题目内容
(理)已知函数f(x)对任意x∈R都有f(x)+f(1-x)=2.
(1)求f(
)和f(
)+f(
)(n∈N*)的值;
(2)数列f(x)满足an=f(0)+f(
)+f(
)+…+f(
)+f(1),(n∈N*)求证:数列{an}是等差数列;
(3)bn=
,Sn=
,Tn=b12+b22+b32+…+bn2,试比较Tn与Sn的大小.
(1)求f(
| 1 |
| 2 |
| 1 |
| n |
| n-1 |
| n |
(2)数列f(x)满足an=f(0)+f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
(3)bn=
| 1 |
| an-1 |
| 4n |
| 2n+1 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用,等差数列与等比数列
分析:(1)分别令x=
,x=
,结合条件,即可求出结果;
(2)令x=
,再应用倒序求和求出an,再由等差数列的定义,即可得证;
(3)先对bn化简,再将bn2放缩,即bn2<2(
-
),再用裂项相消求和,再整理即可得到答案.
| 1 |
| 2 |
| 1 |
| n |
(2)令x=
| k |
| n |
(3)先对bn化简,再将bn2放缩,即bn2<2(
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
(1)解:∵f(x)对任意x∈R都有f(x)+f(1-x)=2,
∴x=
时有f(
)+f(1-
)=2,∴f(
)=1,
令x=
(n∈N*)时有f(
)+f(1-
)=2,∴f(
)+f(
)=2;
(2)证明:f(x)对任意x∈R都有f(x)+f(1-x)=2,
则令x=
时有f(
)+f(
)=2,
∵an=f(0)+f(
)+f(
)+…+f(
)+f(1),
∴an=f(1)+f(
)+f(
)+…+f(
)+f(0),
∴2an=[f(0)+f(1)]+[f(
)+f(
)]+…+[f(
)+f(
)]+[f(1)+f(0)],
∴2an=2(n+1)(n∈N*)
∴an=n+1(n∈N*)
∴an+1-an=(n+2)-(n+1)=1(n∈N*),
∴{an}是等差数列.
(3)解:由(2)有bn=
=
(n∈N*)
∴bn2=
=
<
=
=2(
-
)
∴Tn=b12+b22+b32+…+bn2<2[(1-
)+(
-
)+…+(
-
)]
=2(1-
)=
=Sn
∴Tn<Sn
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令x=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n-1 |
| n |
(2)证明:f(x)对任意x∈R都有f(x)+f(1-x)=2,
则令x=
| k |
| n |
| k |
| n |
| n-k |
| n |
∵an=f(0)+f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
∴an=f(1)+f(
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
∴2an=[f(0)+f(1)]+[f(
| 1 |
| n |
| n-1 |
| n |
| n-1 |
| n |
| 1 |
| n |
∴2an=2(n+1)(n∈N*)
∴an=n+1(n∈N*)
∴an+1-an=(n+2)-(n+1)=1(n∈N*),
∴{an}是等差数列.
(3)解:由(2)有bn=
| 1 |
| an-1 |
| 1 |
| n |
∴bn2=
| 1 |
| n2 |
| 4 |
| 4n2 |
| 4 |
| 4n2-1 |
| 4 |
| (2n+1)(2n-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=b12+b22+b32+…+bn2<2[(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=2(1-
| 1 |
| 2n+1 |
| 4n |
| 2n+1 |
∴Tn<Sn
点评:本题主要考查函数的对称性及应用,同时考查等差数列的定义和通项公式,以及数列求和,及数列不等式的证明:放缩法,是一道综合题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
等差数列{an}中,a1=1,d=1,则该数列的前n项和Sn=( )
| A、n | ||
| B、n(n+1) | ||
| C、n(n-1) | ||
D、
|
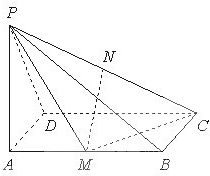 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1. 如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,PA=2,∠ABC=60°,E、F分别为BC、PD的中点.
如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,PA=2,∠ABC=60°,E、F分别为BC、PD的中点.