题目内容
已知函数f(x)=sinx+sin(x+
),x∈[0,π],则f(x)的值域为( )
| π |
| 3 |
A、[-
| ||||||
B、[-
| ||||||
C、[
| ||||||
| D、[-2,2] |
考点:三角函数的最值
专题:三角函数的求值
分析:由条件利用三角函数的恒等变换求得f(x)=
sin(x+
),再根据x∈[0,π],根据正弦函数的定义域和值域,求得f(x)的值域.
| 3 |
| π |
| 6 |
解答:
解:函数f(x)=sinx+sin(x+
)=sinx+
sinx+
cosx=
(
sinx+
cosx)=
sin(x+
),
又x∈[0,π],∴x+
∈[
,
],故当x+
=
时,f(x)取得最小值为
sin
=-
;
当x+
=
时,f(x)取得最小值为
sin
=
,
故函数的值域为[-
,
],
故选:B.
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
又x∈[0,π],∴x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 3 |
| 7π |
| 6 |
| ||
| 2 |
当x+
| π |
| 6 |
| π |
| 2 |
| 3 |
| π |
| 2 |
| 3 |
故函数的值域为[-
| ||
| 2 |
| 3 |
故选:B.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
函数f(x)=
,若f(2)+f(α)=e+1,则α的所有可能值为( )
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是棱BC上的一点,则三棱锥D1-B1C1E的体积等于( )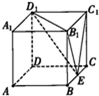

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=2x-
的零点在区间( )
| 1 |
| x |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
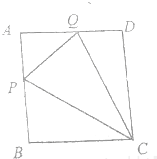 如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).
如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).