题目内容
2.已知函数f(x)=ln(x-2)-$\frac{{x}^{2}}{2a}$,(a为常数且a≠0),若f(x)在x0处取得极值,且x0∉[e+2,e2+2],而f(x)≥0在[e+2,e2+2]上恒成立,则a的取值范围( )| A. | a≥e4+2e2 | B. | a>e2+2e | C. | a≥e2+2e | D. | a>e4+2e2 |
分析 求出原函数的导函数,求得极值点,确定函数的单调性,要使f(x)≥0在[e+2,e2+2]上恒成立,得到关于a的不等式组,求解不等式组可得a的取值范围.
解答 解:由f(x)=ln(x-2)-$\frac{{x}^{2}}{2a}$,得f′(x)=$\frac{1}{x-2}-\frac{x}{a}$(x>2),令f′(x)=0,可得x0=1±$\sqrt{a+1}$,
∵f(x)在x0处取得极值,∴1+$\sqrt{a+1}$>2,即a>0.
∴函数在(2,1+$\sqrt{a+1}$)上单调增,在(1+$\sqrt{a+1}$,+∞)上单调减,
又x0∉[e+2,e2+2],
∴函数在区间[e+2,e2+2]上是单调函数
∴$\left\{\begin{array}{l}{1+\sqrt{a+1}>{e}^{2}+2}\\{f(e+2)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{e+2>1+\sqrt{a+1}}\\{f({e}^{2}+2)≥0}\end{array}\right.$,
解得a>e4+2e2 .
∴a的取值范围是a>e4+2e2 .
故选:D.
点评 本题考查导数知识的运用,考查函数的极值,考查恒成立问题,属于中档题.

练习册系列答案
相关题目
17.曲线y=-$\frac{1}{x}$在(1,-1)处的切线的斜率为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
14.已知双曲线方程为x2-y2=4,过点A(3,1)作直线l与该双曲线交于M,N两点,若点A恰好为MN中点,则直线l的方程为( )
| A. | y=3x-8 | B. | y=-3x+8 | C. | y=3x-10 | D. | y=-3x+10 |
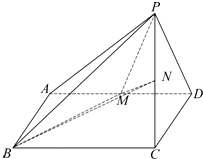 四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.
四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.