题目内容
计算:
(1)5 log59+
log232-log3(log28)
(2)(0.027) -
-(
)-2+(2
)
-(
-1)0.
(1)5 log59+
| 1 |
| 2 |
(2)(0.027) -
| 1 |
| 3 |
| 1 |
| 7 |
| 7 |
| 9 |
| 1 |
| 2 |
| 2 |
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用对数的恒等式、对数的运算法则即可得出;
(2)利用指数幂的运算法则即可得出.
(2)利用指数幂的运算法则即可得出.
解答:
解(1)原式=9+
log225-log33
=9+
-1=
.
(2)原式=(0.33)-
-(7-1)-2+(
)
-1
=
-49+
-1
=-45.
| 1 |
| 2 |
=9+
| 5 |
| 2 |
| 21 |
| 2 |
(2)原式=(0.33)-
| 1 |
| 3 |
| 25 |
| 9 |
| 1 |
| 2 |
=
| 1 |
| 0.3 |
| 5 |
| 3 |
=-45.
点评:本题考查了对数的恒等式、对数的运算法则、指数幂的运算法则,属于基础题.

练习册系列答案
相关题目
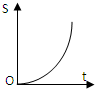
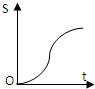
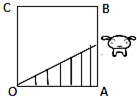 如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )
如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )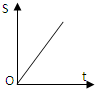
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.