题目内容
8．圆O的半径为3，一条弦AB=4，P为圆O上任意一点，则$\overrightarrow{AB}$•$\overrightarrow{BP}$的取值范围为（ ）| A． | [-16，0] | B． | [0，16] | C． | [-4，20] | D． | [-20，4] |
分析 如图所示，连接OA，OB．过点O作OC⊥AB，垂足为C．利用垂径定理可得BC=$\frac{1}{2}$AB=2．可得cos∠OBA．利用向量的三角形法则，可得$\overrightarrow{AB}$•$\overrightarrow{BP}$=$\overrightarrow{AB}•（\overrightarrow{OP}-\overrightarrow{OB}）$=$\overrightarrow{AB}•\overrightarrow{OP}-\overrightarrow{AB}•\overrightarrow{OB}$，代入数量积即可得出$\overrightarrow{AB}$•$\overrightarrow{BP}$的取值范围．
解答 解：如图所示，连接OA，OB．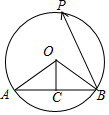
过点O作OC⊥AB，垂足为C．
则BC=$\frac{1}{2}$AB=2．
∴cos∠OBA=$\frac{2}{3}$．
∴$\overrightarrow{AB}$•$\overrightarrow{BP}$=$\overrightarrow{AB}•（\overrightarrow{OP}-\overrightarrow{OB}）$=$\overrightarrow{AB}•\overrightarrow{OP}-\overrightarrow{AB}•\overrightarrow{OB}$
=$|\overrightarrow{AB}||\overrightarrow{OP}|•cos＜\overrightarrow{AB}，\overrightarrow{OP}＞$$-|\overrightarrow{AB}||\overrightarrow{OB}|•cos∠OBA$．
=$4×3×cos＜\overrightarrow{AB}，\overrightarrow{OP}＞-4×3×\frac{2}{3}$=$12cos＜\overrightarrow{AB}，\overrightarrow{OP}＞-8$．
∵cos$＜\overrightarrow{AB}，\overrightarrow{OP}＞$∈[-1，1]，
∴12cos$＜\overrightarrow{AB}，\overrightarrow{OP}＞$-8∈[-20，4]．
故选：D．
点评 本题考查了向量的数量积运算、垂径定理、向量共线定理，属于中档题．
在党的群众交流路线总结阶段，一督导组从某单位随机抽调25名员工，让他们对单位的各项开展公国进行打分评价，现获得如下数据：70，82，81，76，84，77，77，65，85，69，83，71，76，89，74，73，83，78，82，72，86，79，76（1）根据上述数据完成样本的频率分布表；
| 分组 | 频数 | 频率 |
| [65，70] | 3 | 0.12 |
| （70，75] | 5 | 0.20 |
| （75，80] | 8 | 0.32 |
| （80，85] | 7 | 0.28 |
| （85，90] | 2 | 0.08 |
（3）从区间[65，70]和（85，90]中任意抽取两个评分，求两个评分来自不同区间的概率．
