题目内容
14.已知函数f(x)=x2-2xsinθ+1有零点,则θ角的取值集合为{θ|θ=$\frac{π}{2}$+kπ,k∈Z}.分析 函数有零点等价于方程有解,根据根的判别式得到sinθ=±1,即可求出θ的集合
解答 解:∵函数f(x)=x2-2xsinθ+1有零点,
∴x2-2xsinθ+1=0有解,
∴△=4sin2θ-4≥0,
解得sinθ=±1,
∴θ=$\frac{π}{2}$+kπ,k∈Z,
∴θ角的取值集合为{θ|θ=$\frac{π}{2}$+kπ,k∈Z},
故答案为:{θ|θ=$\frac{π}{2}$+kπ,k∈Z}
点评 本题考查了函数的零点和方程解得关系,以及根的判别式和三角函数值,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若在甲袋内装有8个白球、4个红球,在乙袋内装有6个白球、5个红球,现从两袋内各任意取出1个球,设取出的白球个数为X,则下列概率中等于$\frac{{C}_{8}^{1}{C}_{5}^{1}+{C}_{4}^{1}{C}_{6}^{1}}{{C}_{12}^{1}{C}_{11}^{1}}$的是( )
| A. | P(X=0) | B. | P(X≤2) | C. | P(X=1) | D. | P(X=2) |
9.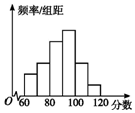 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )| A. | 32 | B. | 27 | C. | 24 | D. | 33 |
19. 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
(1)根据上述数据完成样本的频率分布表;
(2)根据(1)的频率分布表,完成样本频率分布直方图
(3)从区间[65,70]和(85,90]中任意抽取两个评分,求两个评分来自不同区间的概率.
 在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76
在党的群众交流路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展公国进行打分评价,现获得如下数据:70,82,81,76,84,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,86,79,76(1)根据上述数据完成样本的频率分布表;
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | 8 | 0.32 |
| (80,85] | 7 | 0.28 |
| (85,90] | 2 | 0.08 |
(3)从区间[65,70]和(85,90]中任意抽取两个评分,求两个评分来自不同区间的概率.
4.在同一平面直角坐标系中经过伸缩变换$\left\{\begin{array}{l}x'=5x\\ y'=3y\end{array}\right.$后,曲线C变为曲线2x′2+8y′2=1,则曲线C的方程为( )
| A. | 25x2+36y2=1 | B. | 50x2+72y2=1 | C. | 10x2+24y2=1 | D. | $\frac{{2{x^2}}}{25}+\frac{{8{y^2}}}{9}=1$ |