题目内容
 如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.
如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.(Ⅰ)若
| EC |
| EB |
| 1 |
| 3 |
| ED |
| EA |
| 1 |
| 2 |
| DC |
| AB |
(Ⅱ)若EF∥CD,证明:EF2=FA•FB.
考点:与圆有关的比例线段,相似三角形的性质
专题:推理和证明
分析:(Ⅰ)由四点共圆得∠EDC=∠EBF,从而△CED∽△AEB,由此能求出
的值.
(Ⅱ)由平行线性质得∠FEA=∠EDC,由四点共圆得∠EDC=∠EBF,从而△FAE∽△FEB,由此能证明EF2=FA•FB.
| DC |
| AB |
(Ⅱ)由平行线性质得∠FEA=∠EDC,由四点共圆得∠EDC=∠EBF,从而△FAE∽△FEB,由此能证明EF2=FA•FB.
解答:
 (Ⅰ)解:∵A,B,C,D四点共圆,
(Ⅰ)解:∵A,B,C,D四点共圆,
∴∠EDC=∠EBF,
又∵∠CED=∠AEB,∴△CED∽△AEB,
∴
=
=
,∵
=
,
=
,
∴
=
.…(5分)
(Ⅱ)证明:∵EF∥CD,∴∠FEA=∠EDC,
又∵A,B,C,D四点共圆,
∴∠EDC=∠EBF,∴∠FEA=∠EBF,
又∵∠EFA=∠BFE,∴△FAE∽△FEB,
∴
=
,∴EF2=FA•FB…(10分)
 (Ⅰ)解:∵A,B,C,D四点共圆,
(Ⅰ)解:∵A,B,C,D四点共圆,∴∠EDC=∠EBF,
又∵∠CED=∠AEB,∴△CED∽△AEB,
∴
| EC |
| EA |
| ED |
| EB |
| DC |
| AB |
| EC |
| EB |
| 1 |
| 3 |
| ED |
| EA |
| 1 |
| 2 |
∴
| DC |
| AB |
| ||
| 6 |
(Ⅱ)证明:∵EF∥CD,∴∠FEA=∠EDC,
又∵A,B,C,D四点共圆,
∴∠EDC=∠EBF,∴∠FEA=∠EBF,
又∵∠EFA=∠BFE,∴△FAE∽△FEB,
∴
| EF |
| FA |
| FB |
| FE |
点评:本题考查
的值的求法,考查EF2=FA•FB的证明,解题时要认真审题,注意四点共圆的性质的合理运用.
| DC |
| AB |

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
(2-x)8展开式中各项系数的和为( )
| A、-1 | B、1 |
| C、256 | D、-256 |
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是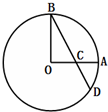 如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=
如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=