题目内容
2.若向量$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),$\overrightarrow{OC}$=(2,1),点O,M,C三点共线,$\overrightarrow{MA}$$•\overrightarrow{MB}$的最小值是-8.分析 根据O,M,C三点共线,得出$\overrightarrow{OM}$=t$\overrightarrow{OC}$,t∈R;
再用坐标表示出$\overrightarrow{MA}$与$\overrightarrow{MB}$,求出$\overrightarrow{MA}$$•\overrightarrow{MB}$的最小值即可.
解答 解:向量$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),$\overrightarrow{OC}$=(2,1),
且O,M,C三点共线,
∴$\overrightarrow{OM}$=t$\overrightarrow{OC}$,t∈R;
∴$\overrightarrow{MA}$=$\overrightarrow{OA}$-$\overrightarrow{OM}$=$\overrightarrow{OA}$-t$\overrightarrow{OC}$=(1-2t,7-t),
$\overrightarrow{MB}$=$\overrightarrow{OB}$-$\overrightarrow{OM}$=$\overrightarrow{OB}$-t$\overrightarrow{OC}$=(5-2t,1-t);
∴$\overrightarrow{MA}$$•\overrightarrow{MB}$=(1-2t)(5-2t)+(7-t)(1-t)=5t2-20t+12=5(t-2)2-8≥-8,
∴$\overrightarrow{MA}$$•\overrightarrow{MB}$的最小值是-8.
故答案为:-8.
点评 本题考查了向量坐标的线性运算与数量积的坐标运算以及二次函数的最值问题,是基础题目.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
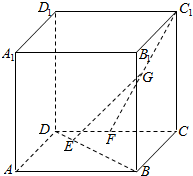 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.



