题目内容
7.已知实数a>0,函数f(x)的定义域为R,则“对任意的x∈R,都有f(x-a)=-f(x)”是“2a是函数f(x)的一个周期”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合函数周期的性质进行判断即可.
解答 解:若对任意的x∈R,都有f(x-a)=-f(x),
则f(x-2a)=-f(x-a)=f(x),则
2a是函数f(x)的一个周期,
若2a是函数f(x)的一个周期,当f(x)=2是周期函数,
但f(x-a)=-f(x)不成立,
即“对任意的x∈R,都有f(x-a)=-f(x)”是“2a是函数f(x)的一个周期”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据函数周期性的定义和性质是解决本题的关键.

练习册系列答案
相关题目
17.数列-1,a,b,c,-9成等比数列,则实数b的值为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 以上都不对 |
18.在(-π,π)内使sinx>cosx成立的x的取值范围是( )
| A. | ($\frac{π}{4}$,π)∪(-$\frac{π}{2}$,-$\frac{π}{4}$) | B. | ($\frac{π}{4}$,π) | C. | ($\frac{π}{4}$,π)∪(-π,-$\frac{3π}{4}$) | D. | (-$\frac{3π}{4}$,π) |
19.过点A(3,2),B(4,3)的直线方程是( )
| A. | x+y+1=0 | B. | x+y-1=0 | C. | x-y+1=0 | D. | x-y-1=0 |
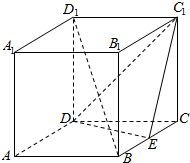 如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.
如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.