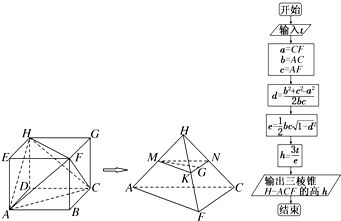
题目内容
下列四种说法:
①垂直于同一平面的所有向量一定共面;
②等差数列{an}中,a1,a3,a4成等比数列,则公比为
;
③已知a>0,b>0,a+b=1,则
+
的最小值为5+2
;
④在△ABC中,已知
=
=
,则∠A=60°.
正确的序号有 .
①垂直于同一平面的所有向量一定共面;
②等差数列{an}中,a1,a3,a4成等比数列,则公比为
| 1 |
| 2 |
③已知a>0,b>0,a+b=1,则
| 2 |
| a |
| 3 |
| b |
| 6 |
④在△ABC中,已知
| a |
| cosA |
| b |
| cosB |
| c |
| cosC |
正确的序号有
考点:命题的真假判断与应用
专题:计算题,等差数列与等比数列,解三角形,不等式的解法及应用
分析:运用线面垂直的性质定理,及平行向量共面,即可判断①;
运用等差数列的通项公式和等比数列的性质,即可求得公比,进而判断②;
运用1的代换,化简整理运用基本不等式即可求得最小值,即可判断③;
运用正弦定理和同角的商数关系,结合内角的范围,即可判断④.
运用等差数列的通项公式和等比数列的性质,即可求得公比,进而判断②;
运用1的代换,化简整理运用基本不等式即可求得最小值,即可判断③;
运用正弦定理和同角的商数关系,结合内角的范围,即可判断④.
解答:
解:对于①垂直于同一平面的所有向量一定平行,而平行向量共面,则①正确;
对于②等差数列{an}中,a1,a3,a4成等比数列,则有a32=a1a4,即有(a1+2d)2=a1(a1+3d),
解得a1=-4d或d=0,则公比为
=1或
,则②错误;
对于③,由于a>0,b>0,a+b=1,则
+
=(a+b)(
+
)=5+
+
≥5+2
=5+2
,
当且仅当
b=
a,取得最小值,且为5+2
,则③正确;
对于④,在△ABC中,
=
=
即为
=
=
,即tanA=tanB=tanC,
由于A,B,C为三角形的内角,则有A=B=C=60°,则④正确.
综上可得,正确的命题有①③④.
故答案为:①③④.
对于②等差数列{an}中,a1,a3,a4成等比数列,则有a32=a1a4,即有(a1+2d)2=a1(a1+3d),
解得a1=-4d或d=0,则公比为
| a3 |
| a1 |
| 1 |
| 2 |
对于③,由于a>0,b>0,a+b=1,则
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| 2b |
| a |
| 3a |
| b |
|
| 6 |
当且仅当
| 2 |
| 3 |
| 6 |
对于④,在△ABC中,
| a |
| cosA |
| b |
| cosB |
| c |
| cosC |
| sinA |
| cosA |
| sinB |
| cosB |
| sinC |
| cosC |
由于A,B,C为三角形的内角,则有A=B=C=60°,则④正确.
综上可得,正确的命题有①③④.
故答案为:①③④.
点评:本题考查正弦定理的运用,考查等差数列和等比数列的通项和性质,考查基本不等式的运用:求最值,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
函数f(x)=ln(x+1)•tanx的图象可能是( )
A、 |
B、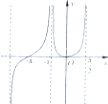 |
C、 |
D、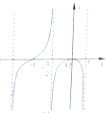 |
阅读如图的程序框图,运行相应的程序,输出的结果为( )


A、-
| ||
B、
| ||
| C、3 | ||
D、
|