题目内容
设函数f(x)=sin(2x+φ)(0<φ<π)的图象的一条对称轴是x=
.
(1)求φ的值及f(x)在区间[0,
]上的最大值和最小值;
(2)若f(α)=
,α∈[
,
],求cos2α的值.
| π |
| 6 |
(1)求φ的值及f(x)在区间[0,
| π |
| 2 |
(2)若f(α)=
| 4 |
| 5 |
| π |
| 4 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据函数的对称轴即可求φ的值及f(x)在区间[0,
]上的最大值和最小值;
(2)根据f(α)=
,α∈[
,
],利用两角和差的余弦公式即可求cos2α的值.
| π |
| 2 |
(2)根据f(α)=
| 4 |
| 5 |
| π |
| 4 |
| π |
| 2 |
解答:
解:(1)f(x)=sin(2x+φ)(0<φ<π)的图象的一条对称轴是x=
.
故f(
)=±1⇒φ=
+kπ,k∈Z
又0<φ<π,故φ=
. …(3分)
所以,f(x)=sin(2x+
).x∈[0,
]⇒2x+
∈[
,
]⇒sin(2x+
)∈[-
,1]
即f(x)在区间[0,
]上的最大值是1,最小值是-
. …(7分)
(2)由已知得sin(2α+
)=
,α∈[
,
]⇒2α+
∈[
,
],
所以cos(2α+
)=-
=-
,
cos2α=cos[(2α+
)-
]=cos(2α+
)cos
+sin(2α+
)sin
=-
×
+
×
=
…(13分)
| π |
| 6 |
故f(
| π |
| 6 |
| π |
| 6 |
又0<φ<π,故φ=
| π |
| 6 |
所以,f(x)=sin(2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
即f(x)在区间[0,
| π |
| 2 |
| 1 |
| 2 |
(2)由已知得sin(2α+
| π |
| 6 |
| 3 |
| 5 |
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
所以cos(2α+
| π |
| 6 |
1-sin2(2α+
|
| 4 |
| 5 |
cos2α=cos[(2α+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=-
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
3-4
| ||
| 10 |
点评:本题主要考查三角函数的图象和性质以及三角函数值的计算,利用条件求出函数的解析式是解决本题的关键.

练习册系列答案
相关题目
直线x+y=1和圆:x2+y2-6x+8y-24=0的位置关系是( )
| A、相切 | B、相交 | C、相离 | D、不确定 |
一个长方体,其正视图面积为
,侧视图面积为
,俯视图面积为
,则长方体的外接球的表面积为( )
| 6 |
| 3 |
| 2 |
| A、6π | ||
| B、24π | ||
C、6
| ||
D、
|
一个正八面体的八个顶点都在同一个球面上,如果该正八面体的棱长为
.则这个球的表面积为( )
| 2 |
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
已知x∈(0,1)时,函数f(x)=
的最小值为b,若定义在R上的函数g(x)满足:对任意m,n∈R都有g(m+n)=g(m)+g(n)+b,则下列结论正确的是( )
| 1+2x2 | ||
2x
|
| A、g(x)-1是奇函数 | ||
| B、g(x)+1是奇函数 | ||
C、g(x)-
| ||
D、g(x)-
|
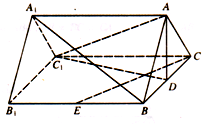 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.