题目内容
已知四面体ABCD满足AB=BC=AD=1，BD=AC=
，BC⊥AD，则该四面体外接球的表面积等于 ．
| 2 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：由线面垂直的判定定理可得BC⊥平面ABD，则BC⊥BD，取CD中点O，连接OB，OA，由直角三角形斜边上的中线等于斜边的一半，即可得到球的半径，进而得到球的表面积．
解答：
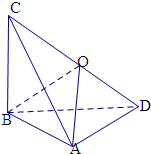解：由于AB=BC=AD=1，BD=AC=
，
则AB⊥BC，
又BC⊥AD，
则BC⊥平面ABD，
则BC⊥BD，
则CD=
=
，
取CD中点O，连接OB，OA，
由直角三角形斜边上的中线等于斜边的一半，
则OA=OB=OC=OD=
，
则该四面体外接球的球心即为O，
则球的表面积为S=4πr2=4π×（
）2=3π．
故答案为：3π．
解：由于AB=BC=AD=1，BD=AC=| 2 |
则AB⊥BC，
又BC⊥AD，
则BC⊥平面ABD，
则BC⊥BD，
则CD=
| 1+2 |
| 3 |
取CD中点O，连接OB，OA，
由直角三角形斜边上的中线等于斜边的一半，
则OA=OB=OC=OD=
| ||
| 2 |
则该四面体外接球的球心即为O，
则球的表面积为S=4πr2=4π×（
| ||
| 2 |
故答案为：3π．
点评：本题考查线面垂直的判定和性质，考查直角三角形的性质，考查球的表面积计算，求出球的半径是解题的关键．
练习册系列答案
相关题目
下面说法正确的是（ ）
| A、命题“?x∈R，使得x2+x+1≥0”的否定是“?x∈R，使得x2+x+1≥0” |
| B、实数x＞y是x2＞y2成立的充要条件 |
| C、设p，q为简单命题，若“p∨q”为假命题，则“￢p∧￢q”也为假命题 |
| D、命题“若cosα≠1，则α≠0”的逆否命题为真命题 |
动点P（x，y）满足方程
=
，则动点P的轨迹是（ ）
| (x+2)2+(y-2)2 |
| |x-y+3| | ||
|
| A、直线 | B、双曲线 |
| C、椭圆 | D、抛物线 |
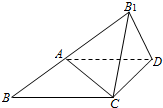已知四边形ABCD是矩形，BC=