题目内容
11.已知f(θ)=$\frac{sin(θ-\frac{π}{2})cos(\frac{3π}{2}+θ)tan(π-θ)}{tan(-π-θ)sin(-π-θ)}$,g(θ)=$\frac{sin(2π-θ)cos(π+θ)cos(\frac{π}{2}+θ)cos(\frac{11π}{2}-θ)}{cos(π-θ)sin(3π-θ)sin(-π-θ)sin(\frac{9π}{2}+θ)}$(Ⅰ)化简f(θ),g(θ)
(Ⅱ)若f(θ)>0,g(θ)<0,试确定角θ所在的象限.
分析 (Ⅰ)利用诱导公式化简求值即可得解.
(Ⅱ)结合三角函数值的符合判断即可得解.
解答 解:(Ⅰ)f(θ)=$\frac{sin(θ-\frac{π}{2})cos(\frac{3π}{2}+θ)tan(π-θ)}{tan(-π-θ)sin(-π-θ)}$=$\frac{cosθsinθ(-tanθ)}{(-tanθ)sinθ}$=cosθ,
g(θ)=$\frac{sin(2π-θ)cos(π+θ)cos(\frac{π}{2}+θ)cos(\frac{11π}{2}-θ)}{cos(π-θ)sin(3π-θ)sin(-π-θ)sin(\frac{9π}{2}+θ)}$=$\frac{(-sinθ)(-cosθ)(-sinθ)(-sinθ)}{(-cosθ)sinθsinθcosθ}$=-tanθ.
(Ⅱ)解:∵f(θ)=cosθ>0,
∴θ在第一象限或第四象限,
∵g(θ)=-tanθ<0,可得tanθ>0,
∴θ在第一象限或第三象限,
综上:θ在第一象限.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,由三角函数值的符号判断角的终边位置,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
20.某单位有职工200人,其年龄分布如下表:
为了解该单位职工的身体健康状况,用分层抽样的方法抽取一个容量为40的样本进行调查,则年龄在[30,40]内的职工应抽取的人数为18.
| 年龄(岁) | [20,30] | [30,40] | [40,60] |
| 人数 | 70 | 90 | 40 |
8.复数z=$\frac{2i}{1+i}$的共轭复数是( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
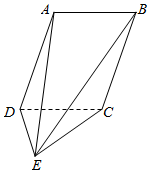 如图,平行四边形ABCD⊥平面CDE,AD⊥DE.
如图,平行四边形ABCD⊥平面CDE,AD⊥DE.