题目内容
6.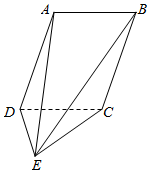 如图,平行四边形ABCD⊥平面CDE,AD⊥DE.
如图,平行四边形ABCD⊥平面CDE,AD⊥DE.(I)求证:DE⊥平面ABCD;
(Ⅱ)若M为线段BE中点,N为线段CE的一个三等分点,求证:MN不可能与平面ABCD平行.
分析 (1)在平面ABCD内过A作CD的垂线AP,则AP⊥平面CDE,于是AP⊥DE,结合AD⊥DE,得出DE⊥平面ABCD;
(2)使用反证法证明,假设MN∥平面ABCD,由线面平行的性质得MN∥BC,与已知矛盾.
解答 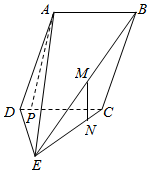 证明:(1)过A作AP⊥CD,垂足为P,
证明:(1)过A作AP⊥CD,垂足为P,
∵平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,AP?平面ABCD,AP⊥CD,
∴AP⊥平面CDE,∵DE?平面CDE,
∴AP⊥DE,又∵DE⊥AD,AD?平面ABCD,AP?平面ABCD,AD∩AP=A,
∴DE⊥平面ABCD.
(2)假设MN∥平面ABCD,
∵MN?平面BCE,平面BCE∩平面ABCD=BC,
∴MN∥BC,
∴$\frac{EM}{EB}=\frac{EN}{EC}$,
与M是BE的中点,N是CE的三等分点相矛盾.
∴MN不可能与平面ABCD平行.
点评 本题考查了线面垂直的判定,线面平行的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在正三棱锥V-ABC中,底面边长为3,三棱锥的高是3,D是VC的中点,则异面直线BD和VA所成角的余弦值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{10}}{8}$ | D. | $\frac{\sqrt{10}}{5}$ |
1.为研究变量x和y的线性相关关系,甲、乙二人分别做了研究,利用线性回归方法得到回归直线l1和l2,由两人计算知,x相同,y也相同,则l1与l2的关系为( )
| A. | 垂直 | B. | 平行 | C. | 相交于点($\overline{x}$,$\overline{y}$) | D. | 重合 |
18.已知{an}是等差数列,a1≠d,则a2+a8≠( )
| A. | a1+a9 | B. | a4+a6 | C. | 2a5 | D. | a1+a3+a6 |
3.设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A⊆B的B的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |