题目内容
求不等式的解集：4x2-20x＜25．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：首先把一元二次不等式转化为标准形式，进一步利用一元二次方程的根确定一元二次不等式的解集．
解答：
解：4x2-20x＜25转化为：4x2-20x-25＜0
令4x2-20x-25=0
解得：x1，2=
=
所以：4x2-20x-25＜0的解集为：{x|
＜x＜
}
令4x2-20x-25=0
解得：x1，2=
20±
| ||
| 8 |
5±5
| ||
| 2 |
所以：4x2-20x-25＜0的解集为：{x|
5-5
| ||
| 2 |
5+5
| ||
| 2 |
点评：本题考查的知识要点：一元二次方程与一元二次不等式的关系．
练习册系列答案
相关题目
已知全集U=R，集合A={x||x|＜3}，B={x|x-2≥0}，则A∪∁UB等于（ ）
| A、（-∞，3] |
| B、（-∞，3） |
| C、[2，3） |
| D、（-3，2] |
下列命题中正确的是（ ）
| A、一直线与一平面平行，这个平面内有无数条直线与它平行 |
| B、平行于同一直线的两个平面平行 |
| C、与两相交平面的交线平行的直线必平行于这两个相交平面 |
| D、两条平行直线中的一条与一个平面平行，则另一条也与该平面平行 |
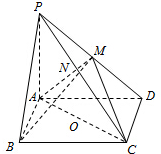在四棱锥P-ABCD中，底面ABCD是矩形PA⊥ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N．