题目内容
已知关于x的二次函数f(x)=ax2-4bx+1.
(Ⅰ)设集合A={-1,1,2,3,4,5}和B={-2,-1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
(Ⅰ)设集合A={-1,1,2,3,4,5}和B={-2,-1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域
|
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)分a=1,2,3,4,5 这五种情况来研究a>0,且
≤1的取法共有16种,而所有的取法共有6×6=36 种,从而求得所求事件的概率.
(Ⅱ)由条件可得,实验的所有结果构成的区域的面积等于S△OMN=
×8×8=32,满足条件的区域的面积为S△POM=
×8×
=
,故所求的事件的概率为 P=
,运算求得结果.
| 2b |
| a |
(Ⅱ)由条件可得,实验的所有结果构成的区域的面积等于S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 32 |
| 3 |
| S△POM |
| S△OMN |
解答:
解:要使函数y=f(x)在区间[1,+∞)上是增函数,则a>0且-
≤1,即a>0且2b≤a.
(Ⅰ)所有(a,b)的取法总数为6×6=36个,满足条件的(a,b)有(1,-2),(1,-1),(2,-2),(2,-1),(2,1),(3,-2),(3,-1),(3,1),(4,-2),(4,-1),(4,1),(4,2),(5,-2),(5,-1),(5,1),(5,2)共16个,
所以,所求概率p=
=
.…(6分)
(Ⅱ)如图,求得区域
的面积为
×8×8=32.
由
,求得P(
,
)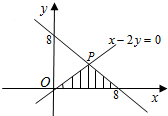
所以区域内满足a>0且2b≤a的面积为
×8×
=
.
所以,所求概率p=
=
.
| -4b |
| 2a |
(Ⅰ)所有(a,b)的取法总数为6×6=36个,满足条件的(a,b)有(1,-2),(1,-1),(2,-2),(2,-1),(2,1),(3,-2),(3,-1),(3,1),(4,-2),(4,-1),(4,1),(4,2),(5,-2),(5,-1),(5,1),(5,2)共16个,
所以,所求概率p=
| 16 |
| 36 |
| 4 |
| 9 |
(Ⅱ)如图,求得区域
|
| 1 |
| 2 |
由
|
| 16 |
| 3 |
| 8 |
| 3 |

所以区域内满足a>0且2b≤a的面积为
| 1 |
| 2 |
| 8 |
| 3 |
| 32 |
| 3 |
所以,所求概率p=
| ||
| 32 |
| 1 |
| 3 |
点评:本题考查了等可能事件的概率与二次函数的单调区间以及简单的线性规划问题相结合的问题,画出实验的所有结果构成的区域,Ⅰ是古典概型的概率求法,Ⅱ是几何概型的概率求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数
所对应的点位于复平面内( )
| 2i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,∠A=30°,AB=4,满足此条件的△ABC有两解,则BC边长度的取值范围为( )
A、(2
| ||
| B、(2,4) | ||
| C、(4,+∞) | ||
D、(2
|
若曲线y=
与直线y=kx+1有两个不同的交点,则实数k的取值范围是( )
|
A、(-3-2
| ||||
B、(-3+2
| ||||
C、(-∞,-3-2
| ||||
D、(-3-2
|
 如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°).
如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°).