题目内容
给出下列命题:
①已知a,b,m都是正数,且
>
,则a<b;
②当x∈(1,+∞)时,函数y=x3,y=x
的图象都在直线y=x的上方;
③命题“?x∈R,使得x2-2x+1<0”的否定是真命题;
④“x≤1,且y≤1”是“x+y≤2”的充要条件.
其中正确命题的序号是 (把你认为正确命题的序号都填上).
①已知a,b,m都是正数,且
| a+1 |
| b+1 |
| a |
| b |
②当x∈(1,+∞)时,函数y=x3,y=x
| 1 |
| 2 |
③命题“?x∈R,使得x2-2x+1<0”的否定是真命题;
④“x≤1,且y≤1”是“x+y≤2”的充要条件.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:阅读型
分析:①已知a,b,m都是正数,且
>
,根据不等式的性质不难得出结论;
②分别判定当x∈(1,+∞)时,函数y=x3,y=x
的图象的位置,可直接得出结论;
③先给出命题“?x∈R,使得x2-2x+1<0”的否定,再判定即可得出结论;
④根据充要条件的概念举例即可进行判定.
| a+1 |
| b+1 |
| a |
| b |
②分别判定当x∈(1,+∞)时,函数y=x3,y=x
| 1 |
| 2 |
③先给出命题“?x∈R,使得x2-2x+1<0”的否定,再判定即可得出结论;
④根据充要条件的概念举例即可进行判定.
解答:
解:①已知a,b,m都是正数,且
>
,所以ab+b>ab+a化简可得a<b;故正确.
②因为当x∈(1,+∞)时,函数y=x3的图象都在直线y=x的上方;但函数y=x
的图象都在直线y=x的下方;故②错误.
③命题“?x∈R,使得x2-2x+1<0”的否定是“?x∈R,使得x2-2x+1≥0”
∵a>0开口向上,顶点为(1,0)由图象知这显然是个真命题;故正确.
④举例1.5+0.1≤2,而1.5>1,显然错误.
故答案为:①③
| a+1 |
| b+1 |
| a |
| b |
②因为当x∈(1,+∞)时,函数y=x3的图象都在直线y=x的上方;但函数y=x
| 1 |
| 2 |
③命题“?x∈R,使得x2-2x+1<0”的否定是“?x∈R,使得x2-2x+1≥0”
∵a>0开口向上,顶点为(1,0)由图象知这显然是个真命题;故正确.
④举例1.5+0.1≤2,而1.5>1,显然错误.
故答案为:①③
点评:本题从概念和图象出发不难得出结论,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
则f(f(-2))( )
|
| A、16 | ||
B、
| ||
| C、4 | ||
D、
|
设U=R,A={x|x>0},B={x|x>1},则A∪B=( )
| A、{x|0≤x<1} |
| B、{x|0<x≤1} |
| C、{x|x>0} |
| D、{x|x>1} |
i是虚数单位,若复数z=
,则复数z的实部与虚部的和是( )
| 3+i |
| 1-i |
| A、3 | B、1+2i |
| C、2 | D、1-2i |
cos420°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
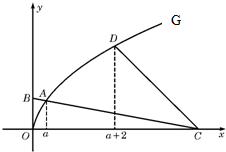 如图,曲线G的方程为y=
如图,曲线G的方程为y=