题目内容
已知函数f(x)=x3+ax2+bx+c(x∈[-1,2]),且函数f(x)在x=1和x=-
处都取得极值.
(1)求实数a,b的值;
(2)求函数f(x)的极值;
(3)若对任意x∈[-1,1],f(x)<c2,恒成立,求实数c的取值范围.
| 2 |
| 3 |
(1)求实数a,b的值;
(2)求函数f(x)的极值;
(3)若对任意x∈[-1,1],f(x)<c2,恒成立,求实数c的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求出函数的导数,得出方程组,解出a,b即可;
(2)作出x,f′(x),f(x)的变化表格,得出x∈[-1,2]时,f(x)的最大值为f(2)=2+c;
(3)由题意得只需c2>2+c,解不等式即可.
(2)作出x,f′(x),f(x)的变化表格,得出x∈[-1,2]时,f(x)的最大值为f(2)=2+c;
(3)由题意得只需c2>2+c,解不等式即可.
解答:
解:(1)f'(x)=3x2+2ax+b
由题意可知
,解得
;
(2)由(1)知f'(x)=3x2-x-2=(3x+2)(x-1),
∵f(2)=2+c,
∴x∈[-1,2]时,f(x)的最大值为f(2)=2+c;
(3)∵对于任意的x∈[-1,1],f(x)<c2恒成立,
∴只需c2>2+c,
∴c<-1或c>2.
由题意可知
|
|
(2)由(1)知f'(x)=3x2-x-2=(3x+2)(x-1),
| x | (-1,-
| -
| (-
| 1 | (1,2) | ||||||
| f'(x) | + | 极大值 | - | 极小值 | + | ||||||
| f(x) | ↑ | c+
| ↓ | c-
| ↑ |
∴x∈[-1,2]时,f(x)的最大值为f(2)=2+c;
(3)∵对于任意的x∈[-1,1],f(x)<c2恒成立,
∴只需c2>2+c,
∴c<-1或c>2.
点评:本题考查了函数的单调性,函数的最值问题,考查导数的应用,求参数的范围,本题属于中档题.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的以5为周期的奇函数,若f(3)>0,f(2012)=(a+2)(a-2),则a的取值范围是( )
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-2,2) |
| D、(-∞,-2)∪(2,+∞) |
cos420°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 已知f(x)=2cos2x+2
已知f(x)=2cos2x+2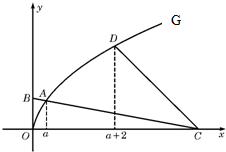 如图,曲线G的方程为y=
如图,曲线G的方程为y=