题目内容
将5封信随意投入3个不同的邮箱里，每个邮箱中的信件不限，共有（ ）种不同的投法．
| A、5+3=8 |
| B、5×3=15 |
| C、53=125 |
| D、35=243 |
考点：计数原理的应用
专题：排列组合
分析：从5封信中随便取出一分，投入一个邮筒，选择邮筒有3种选择．再拿出第二封信同样有3种选择，第三封信也有3种选择，第四封也有3种，第五封信也有3种选择，那么一共就有种3×3×3×3×3选择的方法．
解答：
解：由分布乘法原理得5封信随意投入3个不同的邮箱里，每个邮箱中的信件不限共有
3×3×3×3×3=35═243（种）；
故答案为：D
3×3×3×3×3=35═243（种）；
故答案为：D
点评：本题运用乘法原理求解，总次数应是每个分步次数的积．本题的考点是排列、组合及简单计数原理，主要考查相同元素的分配问题．
练习册系列答案
相关题目
已知函数f（x）=
则f（f（-2））（ ）
|
| A、16 | ||
B、
| ||
| C、4 | ||
D、
|
设sinα=
（
＜α＜π），tan（π-β）=
，则tan（α-2β）=（ ）
| 3 |
| 5 |
| π |
| 2 |
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f（x）是定义在R上的以5为周期的奇函数，若f（3）＞0，f（2012）=（a+2）（a-2），则a的取值范围是（ ）
| A、（-∞，-2） |
| B、（2，+∞） |
| C、（-2，2） |
| D、（-∞，-2）∪（2，+∞） |
已知非零向量
⊥
，则下列各式正确的是（ ）
| a |
| b |
A、|
| ||||||||
B、|
| ||||||||
C、|
| ||||||||
D、|
|
设U=R，A={x|x＞0}，B={x|x＞1}，则A∪B=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＞0} |
| D、{x|x＞1} |
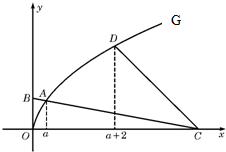如图，曲线G的方程为y=