题目内容
设函数f(x)=
,则函数F(x)=xf(x)-1的零点的个数为( )
|
| A、4 | B、5 | C、6 | D、7 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由F(x)=0得f(x)=
,然后分别作出函数f(x)与y=
的图象,利用数形结合即可得到函数零点的个数.
| 1 |
| x |
| 1 |
| x |
解答:
 解:F(x)=f(x)-
解:F(x)=f(x)-
的)=0得f(x)=
,然后分别作出函数f(x)与y=g(x)=
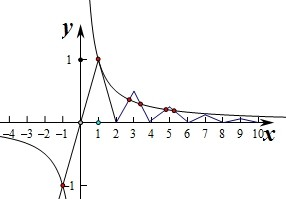
的图象如图:
∵当x≥2时,f(x)=
f(x-2),
∴f(1)=1,g(1)=1,
f(1)=1,g(1)=1,
f(3)=
f(1)=
,g(3)=
,
f(5)=
f(3)=
,g(5)=
,
f(7)=
f(5)=
,g(7)=
,
∴当x>7时,f(x)<
,
由图象可知两个图象的交点个数为6个.
故选:C.
 解:F(x)=f(x)-
解:F(x)=f(x)-| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∵当x≥2时,f(x)=
| 1 |
| 2 |
∴f(1)=1,g(1)=1,
f(1)=1,g(1)=1,
f(3)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
f(5)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 5 |
f(7)=
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 7 |
∴当x>7时,f(x)<
| 1 |
| x |
由图象可知两个图象的交点个数为6个.
故选:C.
点评:本题主要考查函数零点个数的判断,根据方程和函数之间的关系,转化为两个函数图象的交点问题是解决本题的关键,利用数形结合是解决本题的基本思想.本题难度较大,综合性较强.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
代数式
+
+
的所有可能的值有( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、无数个 |
过点M(-1,m),N(m+1,4)的直线的斜率等于1,则m的值为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
已知函数f(x)为偶函数,若将f(x)的图象向右平移一个单位又得到一个奇函数,若f(2)=-1,则f(1)+f(2)+…+f(2013)等于( )
| A、-1 | B、0 |
| C、-1003 | D、1003 |
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
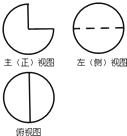

| A、16π | B、14π |
| C、12π | D、8π |
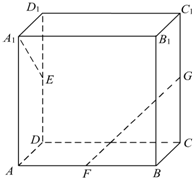 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )