题目内容
已知-1和2是函数y=x2+bx+c的两个零点，则不等式bx2+bx-c＜0的解集为（ ）
| A、（-1，2） |
| B、（-2，1） |
| C、（-∞，-1）∪（2，+∞） |
| D、（2，+∞） |
考点：一元二次不等式的解法,二次函数的性质
专题：不等式的解法及应用
分析：由-1和2是函数y=x2+bx+c的零点，求出b、c的值，从而求出不等式bx2+bx-c＜0的解集．
解答：
解：∵-1和2是函数y=x2+bx+c的两个零点，
∴
，
解得b=-1，c=-2；
∴不等式bx2+bx-c＜0为-x2-x+2＜0，
即（x+1）（x-2）＞0；
解得x＜-1，或x＞2，
∴不等式的解集为（-∞，-1）∪（2，+∞）．
故选：C．
∴
|
解得b=-1，c=-2；
∴不等式bx2+bx-c＜0为-x2-x+2＜0，
即（x+1）（x-2）＞0；
解得x＜-1，或x＞2，
∴不等式的解集为（-∞，-1）∪（2，+∞）．
故选：C．
点评：本题考查了函数的零点与求一元二次不等式的解集的问题，解题时应用一元二次方程根与系数的关系求出b、c的值，是解题的关键．
练习册系列答案
相关题目
将函数图f（x）=sin（x-
）象上的所有点向左平移
个单位长度，则所得图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=cosx |
| C、y=-sinx |
| D、y=-cosx |
如图，在三棱锥S-ABC中，E为棱SC的中点，若AC=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
定义在R上的函数f（x）满足：f（x）+f′（x）＞1，f（0）=4，则不等式exf（x）＞ex+3（其中e为自然对数的底数）的解集为（ ）
| A、（0，+∞） |
| B、（-∞，0）∪（3，+∞） |
| C、（-∞，0）∪（0，+∞） |
| D、（3，+∞） |
已知空间图形的三视图如图，空间几何体的表面积为（ ）
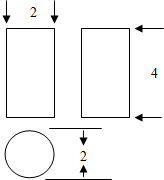
| A、8π | B、10π |
| C、12π | D、9π |
函数y=x|x|的图象经描点确定后的形状大致是（ ）
A、 |
B、 |
C、 |
D、 |
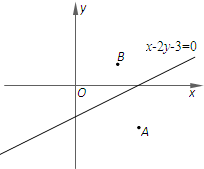已知⊙P经过A（3，-2）、B（2，1）两点，圆心P在直线x-2y-3=0上．