题目内容
设z1、z2∈C，则“z12+z22=0”是“z1=z2=0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：数系的扩充和复数
分析：根据充分条件和必要条件的定义进行判断即可．
解答：
解：若z1=i，z2=1，满足设“z12+z22=0”，但“z1=z2=0”不成立，
若z1=z2=0，则z12+z22=0成立，
故“z12+z22=0”是“z1=z2=0”的必要不充分条件，
故选：B
若z1=z2=0，则z12+z22=0成立，
故“z12+z22=0”是“z1=z2=0”的必要不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据复数的概念是解决本题的关键．
练习册系列答案
相关题目
函数f（x）=
，设f1（x）=f（x），f2（x）=f[f1（x）]，﹒﹒﹒fn（x）=f[fn-1（x）]，（x∈N+，N≥2），令集合M={x|f2008（x）=x2，x∈R}则集合M为（ ）
| x-1 |
| x+1 |
| A、φ | B、实数集 |
| C、单元素集 | D、二元素集 |
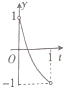
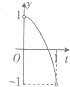
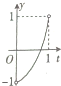
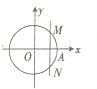在如图所示的直角坐标系中，点A为圆O：x2+y2=1与x轴的交点，垂直于x轴的动直线l从点A出发，以1m/s的速度沿x轴向左移动，记直线l与圆O的交点为M，N，劣弧MN的长为x，令y=cosx，则y与时间t（0＜t＜1，单位：s）的函数y=f（x）的图象大致为（ ）
已知集合M={x|x-2＜0}，N={x|x＜a}，若M⊆N，则实数a的取值范围是（ ）
| A、[2，+∞） |
| B、（2，+∞） |
| C、（-∞，0） |
| D、（-∞，0] |
集合A={x|
≤0}，B={y|y=ln（x-1）}，则A∩B等于（ ）
| x |
| x-1 |
| A、[0，1） | B、∅ |
| C、（0，1） | D、[0，1] |