题目内容
设无穷等比数列{an}的公比为q，若a1=
（a3+a4+…），则q= ．
| lim |
| n→∞ |
考点：等比数列的前n项和,极限及其运算
专题：计算题,等差数列与等比数列
分析：利用无穷等比数列{an}的公比为q，a1=
（a3+a4+…），可得a1=
=
，结合|q|＜1，即可得出结论．
| lim |
| n→∞ |
| a3 |
| 1-q |
| a1q2 |
| 1-q |
解答：
解：∵无穷等比数列{an}的公比为q，a1=
（a3+a4+…），
∴a1=
=
，
∴q2+q-1=0，
∵|q|＜1，∴q=
．
故答案为：
．
| lim |
| n→∞ |
∴a1=
| a3 |
| 1-q |
| a1q2 |
| 1-q |
∴q2+q-1=0，
∵|q|＜1，∴q=
-1+
| ||
| 2 |
故答案为：
-1+
| ||
| 2 |
点评：本题考查无穷等比数列{an}的求和公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
函数f（x）的图象如图所示，则不等式（x+3）•f′（x）＜0的解集为（ ）
| A、（l，+∞） |
| B、（-∞，-3） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，-3）∪（-1，1） |
若向量
=（0，1），
=（2，-1），
=（1，1），则（ ）
| a |
| b |
| c |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、|
|
棱长为2的正方体的外接球的表面积为（ ）
| A、4π | B、12π |
| C、24π | D、48π |
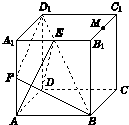如图，在正方体ABCD-A1B1C1D1中，E、F、M分别是棱A1B1、AA1、B1C1的中点．