题目内容
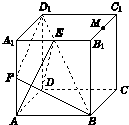 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.(1)求证:BF⊥平面ADE;
(2)是否存在过E、M两点且与平面BFD1平行的平面?若存在,请指出并证明;若不存在,请说明理由.
考点:平面与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)通过证明△ABF≌△A1AE,推出AE⊥BF.然后证明AD⊥BF,利用在与平面垂直的判定定理证明BF⊥平面ADE.
(2)设点N在棱BB1上,且B1N=
BB1,连接ME、NE、MN,则平面EMN∥平面BFD1.证明EN∥A1H,EN∥BF.证明EN∥平面BFD1.MN∥平面BFD1.然后证明平面EMN∥平面BFD1.
(2)设点N在棱BB1上,且B1N=
| 1 |
| 4 |
解答:
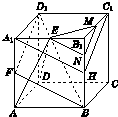 (1)证明:在正方形ABB1A1中,E、F分别是棱A1B1、AA1的中点,
(1)证明:在正方形ABB1A1中,E、F分别是棱A1B1、AA1的中点,
∴△ABF≌△A1AE,∴∠ABF=∠A1AE.∴∠A1AE+∠AFB=∠ABF+∠AFB=90°,∴AE⊥BF.在正方体ABCD-A1B1C1D1中,AD⊥平面ABB1A1,BF?平面ABB1A1,
∴AD⊥BF.∵AE∩AD=A,∴BF⊥平面ADE.
(2)解:如答图,设点N在棱BB1上,且B1N=
BB1,连接ME、NE、MN,则平面EMN∥平面BFD1.证明如下:取BB1的中点H,连接A1H、C1H.
∵E、N分别是A1B1、B1H的中点,∴EN∥A1H.∵A1F∥HB,且A1F=HB,
∴四边形A1FBH是平行四边形.∴A1H∥BF.∴EN∥BF.
∵EN?平面BFD1,BF?平面BFD1,∴EN∥平面BFD1.
同理MN∥平面BFD1.又MN∩EN=N,∴平面EMN∥平面BFD1.
 (1)证明:在正方形ABB1A1中,E、F分别是棱A1B1、AA1的中点,
(1)证明:在正方形ABB1A1中,E、F分别是棱A1B1、AA1的中点,∴△ABF≌△A1AE,∴∠ABF=∠A1AE.∴∠A1AE+∠AFB=∠ABF+∠AFB=90°,∴AE⊥BF.在正方体ABCD-A1B1C1D1中,AD⊥平面ABB1A1,BF?平面ABB1A1,
∴AD⊥BF.∵AE∩AD=A,∴BF⊥平面ADE.
(2)解:如答图,设点N在棱BB1上,且B1N=
| 1 |
| 4 |
∵E、N分别是A1B1、B1H的中点,∴EN∥A1H.∵A1F∥HB,且A1F=HB,
∴四边形A1FBH是平行四边形.∴A1H∥BF.∴EN∥BF.
∵EN?平面BFD1,BF?平面BFD1,∴EN∥平面BFD1.
同理MN∥平面BFD1.又MN∩EN=N,∴平面EMN∥平面BFD1.
点评:本题考查直线与平面垂直的判定定理,平面与平面平行的判定定理的证明,考查空间想象能力逻辑推理能力.

练习册系列答案
相关题目
直线
x-3y+5=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
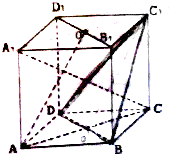 如图,在正方体ABCD-A1B1C1D1中,O是面对角线B1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,O是面对角线B1D1的中点. 执行如图所示的程序框图,如果输入-2,那么输出的结果是
执行如图所示的程序框图,如果输入-2,那么输出的结果是