题目内容
17.已知$\frac{π}{4}<x<\frac{π}{2}$,设a=sinx,b=cosx,c=tanx,则( )| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | b<c<a |
分析 在限定条件下,比较几个式子的大小,用特殊值代入法.
解答 解:$\frac{π}{4}<x<\frac{π}{2}$,
不妨设x=$\frac{π}{3}$,则 sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,cos$\frac{π}{3}$=$\frac{1}{2}$,tan$\frac{π}{3}$=$\sqrt{3}$,
∴cos$\frac{π}{3}$<sin$\frac{π}{3}$<tan$\frac{π}{3}$,
即cosα<sinα<tanα;
又a=sinx,b=cosx,c=tanx,
∴b<a<c.
故选:B.
点评 本题考查了三角函数线,利用特殊值代入法比较大小,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.将函数y=sin(2x+$\frac{π}{6}$)图象上的点M(θ,$\frac{\sqrt{3}}{2}$)(0<θ<$\frac{π}{4}$)向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则( )
| A. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{12}$ | B. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{6}$ | ||
| C. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{6}$ | D. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{12}$ |
9.“(x-1)(x+2)=0”是“x=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知函数f(x)=sin(ωx+$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx-$\frac{7π}{6}$)(ω>0),满足f(-$\frac{π}{6}$)=$\frac{3}{4}$,则满足题意的ω的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
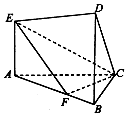 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB