题目内容
已知函数f（x）=ax3+bx2，当x=1时，函数有极大值3．
（1）求函数f（x）的解析式；
（2）求函数f（x）的极小值．
（1）求函数f（x）的解析式；
（2）求函数f（x）的极小值．
考点：利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题：综合题,导数的综合应用
分析：（1）由题意可得，f′（1）=0，f（1）=3，从而得到方程组，解出即可；
（2）解方程f′（x）=0，然后判断导数在方程根的左右两侧的符号可判断极值点，进而可求极小值；
（2）解方程f′（x）=0，然后判断导数在方程根的左右两侧的符号可判断极值点，进而可求极小值；
解答：
解：（1）f′（x）=3ax2+2bx，
当x=1时，f′（1）=3a+2b=0，f（1）=3，
∴
，解得a=-6，b=9，
∴函数解析式为：y=-6x3+9x2．
（2）由（1）知f（x）=-6x3+9x2，
f′（x）=-18x2+18x，令f′（x）＞0，得0＜x＜1；令f′（x）＜0，得x＞1或x＜0，
∴当x=0时函数取得极小值为0．
当x=1时，f′（1）=3a+2b=0，f（1）=3，
∴
|
∴函数解析式为：y=-6x3+9x2．
（2）由（1）知f（x）=-6x3+9x2，
f′（x）=-18x2+18x，令f′（x）＞0，得0＜x＜1；令f′（x）＜0，得x＞1或x＜0，
∴当x=0时函数取得极小值为0．
点评：该题考查利用导数研究函数的极值．求解函数解析式，属中档题．
练习册系列答案
相关题目
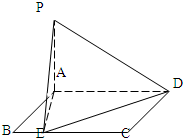如图，四边形ABCD为矩形，且AD=4，AB=2，PA=1，PA⊥平面ABCD，E为线段BC上的动点．