题目内容
10．在△ABC中，A=60°，b=1，c=4，则$\frac{a}{sinA}$=$\frac{{2\sqrt{39}}}{3}$．分析 利用余弦定理求出a，即可求解．
解答 解：∵A=60°，b=1，c=4，
由余弦定理：cosA=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}$，
可得：a=$\sqrt{13}$．
∴$\frac{a}{sinA}$=$\frac{\sqrt{13}}{sin60°}=\frac{2\sqrt{39}}{3}$．
故答案为：$\frac{2\sqrt{39}}{3}$．
点评 本题主要考查了余弦定理的运用和计算能力．属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20．计算sin5°cos55°-cos175°sin125°的结果是（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
1．已知集合A={x∈N|0≤x≤4}，则下列说法正确的是（ ）
| A． | 0∉A | B． | 1⊆A | C． | $\sqrt{2}⊆A$ | D． | 3∈A |
18．椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1上点到直线x+2y-10=0的距离最小值为（ ）
| A． | $\frac{\sqrt{5}}{5}$ | B． | $\sqrt{5}$ | C． | $\frac{6\sqrt{5}}{5}$ | D． | 0 |
15．正方形ABCD，沿对角线BD折成直二面角A-BD-C，则折后的异面直线AB与CD所成的角的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
2．用数学归纳法证明（n+1）（n+2）（n+3）…（n+n）=2n×1×3×…×（2n-1）（n∈N*）时，从n=k（k∈N*）到n=k+1时左边需增乘的代数式是（ ）
| A． | 2k+1 | B． | 2（2k+1） | C． | $\frac{2k+1}{k+1}$ | D． | $\frac{2k+3}{k+1}$ |
19．圆C1：x2+y2-4x-2y+1=0与圆C2：x2+y2+4x-8y+11=0的位置关系为（ ）
| A． | 相交 | B． | 相离 | C． | 外切 | D． | 内切 |
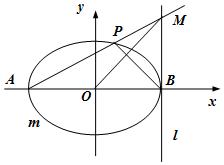已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{1}{2}$，且过点$E（{1，\frac{3}{2}}）$．