题目内容
在Rt△ABC中,若∠C=90°,AC=b,BC=a,斜边AB上的高为h,则有结论h2=
,运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,且三棱锥的直角顶点到底面的高为h,则有结论: .
| a2b2 |
| a2+b2 |
考点:类比推理
专题:推理和证明
分析:由平面上的直角三角形Rt△ABC中的边与高的关系式,类比立体中两两垂直的棱的三棱锥中边与高的关系即可.
解答:
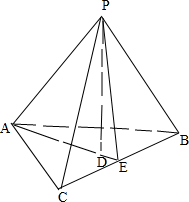 解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,
解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,
连接AD交BC于E,
∵PA、PB、PC两两互相垂直,
∴PA⊥平面PBC,PE?平面PBC,
∴PA⊥PE,PA⊥BC,
∴AE⊥BC,PE⊥BC
∴PE2=
,
∴h2=PD2=
=
=h=
.
故答案为:h=
.
 解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,
解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,连接AD交BC于E,
∵PA、PB、PC两两互相垂直,
∴PA⊥平面PBC,PE?平面PBC,
∴PA⊥PE,PA⊥BC,
∴AE⊥BC,PE⊥BC
∴PE2=
| b2c2 |
| b2+c2 |
∴h2=PD2=
| PA2PE2 |
| PA2+PE2 |
=
a2•
| ||
a2+
|
=h=
| a2b2c2 |
| a2b2+b2c2+c2a2 |
故答案为:h=
| a2b2c2 |
| a2b2+b2c2+c2a2 |
点评:本题主要考查了类比推理的思想和方法,考查运算求解能力,解答此类问题的关键是根据所给的定理类比出立体中两两垂直的棱的三棱锥中边与高的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某项活动从甲、乙、丙、丁四人中任选两名参加,甲被选中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表: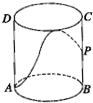 如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为
如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为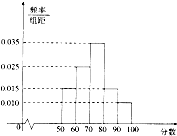 某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为
某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为