题目内容
如果四面体的四条高交于一点，那么这个四面体为垂心四面体，这一点称为四面体的垂心．关于垂心四面体下列命题正确的有 ．（写出所有正确命题的序号）
①正四面体是垂心四面体；
②四面体的垂心就是四面体内切球的球心；
③垂心四面体对棱互相垂直；
④垂心四面体的一条高通过底面的垂心；
⑤垂心四面体对棱的平方和相等．
①正四面体是垂心四面体；
②四面体的垂心就是四面体内切球的球心；
③垂心四面体对棱互相垂直；
④垂心四面体的一条高通过底面的垂心；
⑤垂心四面体对棱的平方和相等．
考点：命题的真假判断与应用,棱柱的结构特征
专题：新定义,空间位置关系与距离
分析：由正四面体的定义和垂心四面体，即可判断①；垂心到四个面的距离相等即为正四面体，即可判断②；由线面垂直的判定和性质，即可判断③；设A在平面BCD上的射影为F，由③和垂心的定义，即可判断④；设BF交CD于E，由勾股定理，即可判断⑤．
解答：
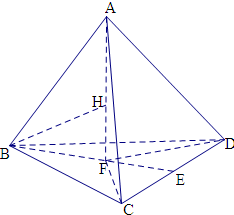解：①正四面体是四个面均为等边三角形的三棱锥，对照定义显然是垂心四面体，故①对；
②四面体的垂心到四个面的距离不一定相等，若相等即为正四面体，故②错；
③ABCD是垂心四面体，设垂心为H，则AH，BH均与CD垂直，则CD垂直于平面ABH，从而AB⊥CD，同理，AC⊥BD，AD⊥BC，
故③对；
④设A在平面BCD上的射影为F，因AB⊥CD，所以AB的射影
BF⊥CD，同理CF⊥BD，即F为△BCD的垂心．故④对；
⑤设BF交CD于E，则AC2-AD2=CF2-DF2=CE2-DE2=BC2-BD2，
即AC2+BD2=AD2+BC2，故⑤对．
故答案为：①③④⑤．
解：①正四面体是四个面均为等边三角形的三棱锥，对照定义显然是垂心四面体，故①对；②四面体的垂心到四个面的距离不一定相等，若相等即为正四面体，故②错；
③ABCD是垂心四面体，设垂心为H，则AH，BH均与CD垂直，则CD垂直于平面ABH，从而AB⊥CD，同理，AC⊥BD，AD⊥BC，
故③对；
④设A在平面BCD上的射影为F，因AB⊥CD，所以AB的射影
BF⊥CD，同理CF⊥BD，即F为△BCD的垂心．故④对；
⑤设BF交CD于E，则AC2-AD2=CF2-DF2=CE2-DE2=BC2-BD2，
即AC2+BD2=AD2+BC2，故⑤对．
故答案为：①③④⑤．
点评：本题考查新定义及理解，考查正四面体的概念，同时考查直线与平面垂直的判定和性质及运用，考查勾股定理的运用，属于中档题．
练习册系列答案
相关题目