题目内容
若命题“?x∈[1,3],x2-ax+4≥0”是真命题,则a的取值范围是 .
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:命题“?x∈[1,3],x2-ax+4≥0”是真命题?a≤x+
(1≤x≤3)恒成立,令g(x)=x+
(1≤x≤3),利用基本不等式易求g(x)min=4,从而可得a的取值范围.
| 4 |
| x |
| 4 |
| x |
解答:
解:∵当x∈[1,3]时,x2-ax+4≥0恒成立,
∴a≤x+
(1≤x≤3)恒成立,令g(x)=x+
(1≤x≤3),
则a≤g(x)min,
∵x+
≥2
=4(当且仅当x=2时取“=”),
∴g(x)min=4,
∴a≤4.
故答案为:(-∞,4].
∴a≤x+
| 4 |
| x |
| 4 |
| x |
则a≤g(x)min,
∵x+
| 4 |
| x |
x•
|
∴g(x)min=4,
∴a≤4.
故答案为:(-∞,4].
点评:本题考查恒成立问题,着重考查构造函数的思想与等价转化思想的综合运用,考查基本不等式,属于中档题.

练习册系列答案
相关题目
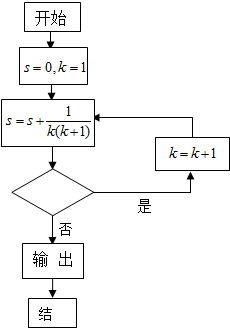
若如图所示的框图所给程序运行的结果S=
,那么判断框中可以填入的关于实数k的判断条件应是( )
| 2010 |
| 2011 |

| A、k<2010 |
| B、k<2009 |
| C、k>2010 |
| D、k>2009 |