题目内容
有下列四个命题
①“若b=3,则b2=9”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若c≤1,则x2+2x+c=0有实根”;
④“若A∪B=A,则A⊆B”的逆否命题.
其中真命题的个数是( )
①“若b=3,则b2=9”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若c≤1,则x2+2x+c=0有实根”;
④“若A∪B=A,则A⊆B”的逆否命题.
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:写出其逆命题,可判断①;写出否命题,举例即可判断②;由二次方程的判别式的符号,即可判断③
由集合的运算性质:A∪B=A,则A⊆B,即可判断原命题的真假,再由互为逆否命题的两命题的等价性,可判断④.
由集合的运算性质:A∪B=A,则A⊆B,即可判断原命题的真假,再由互为逆否命题的两命题的等价性,可判断④.
解答:
解:①“若b=3,则b2=9”的逆命题是“若b2=9,则b=3”,显然错的;
②“全等三角形的面积相等”的否命题是“不全等的三角形,其面积不相等”,
比如同底等高的三角形,面积相等,故②错;
③方程x2+2x+c=0的判别式为△=4-4c,若c≤1,则△≥0,故③对;
④若A∪B=A,则B⊆A,则命题“若A∪B=A,则A⊆B”为假命题,由逆否命题的等价性
可知其逆否命题也为假命题.
故选A.
②“全等三角形的面积相等”的否命题是“不全等的三角形,其面积不相等”,
比如同底等高的三角形,面积相等,故②错;
③方程x2+2x+c=0的判别式为△=4-4c,若c≤1,则△≥0,故③对;
④若A∪B=A,则B⊆A,则命题“若A∪B=A,则A⊆B”为假命题,由逆否命题的等价性
可知其逆否命题也为假命题.
故选A.
点评:本题考查四种命题及真假判断,注意运用互为逆否命题的两命题的等价性,本题属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
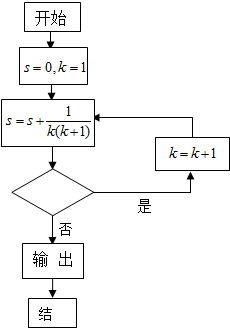
若如图所示的框图所给程序运行的结果S=
,那么判断框中可以填入的关于实数k的判断条件应是( )
| 2010 |
| 2011 |

| A、k<2010 |
| B、k<2009 |
| C、k>2010 |
| D、k>2009 |
已知a,b是实数,则“|a-b|≥a+b”是“ab<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设{an}是首项大于零的等比数列,则“a1>a2”是“数列{an}为递减数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若抛物线y2=ax经过不等式组
表示的平面区域,则抛物线焦点的横坐标的取值范围是( )
|
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
△ABC中B=
且sinA:sinC=3:1,则b:c的值为( )
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、7 |
 如图,将边长为2的正方形ABCD沿对角线BD折起得到一个三棱锥C-ABD,已知该三棱锥的正视图与俯视图如图所示,则其侧视图的面积为( )
如图,将边长为2的正方形ABCD沿对角线BD折起得到一个三棱锥C-ABD,已知该三棱锥的正视图与俯视图如图所示,则其侧视图的面积为( )