题目内容

若1、a、b、c、9成等比数列，则b=
 
．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据等比数列的定义和性质可得b＞0，且ac=b2=1×9=9，即可求出的值．
解答： 解：若1、a、b、c、9成等比数列，则b＞0，且ac=b2=1×9=9，
∴b=3．
故答案为：3．
点评：本题主要考查等比数列的定义和性质，判断b＞0，且ac=b2=1×9=9是解题的关键．
练习册系列答案
相关题目
已知不等式5ij≤ki2+2j2对于所有i，j∈{1，2，3}都成立，则实数k的取值范围是
 
．
如果四面体的四条高交于一点，那么这个四面体为垂心四面体，这一点称为四面体的垂心．关于垂心四面体下列命题正确的有
 
．（写出所有正确命题的序号）
①正四面体是垂心四面体；
②四面体的垂心就是四面体内切球的球心；
③垂心四面体对棱互相垂直；
④垂心四面体的一条高通过底面的垂心；
⑤垂心四面体对棱的平方和相等．
（理科）定义运算x*y=
x(x≤y)
y(x＞y)
，若（2x-1）*x＜2，则x的取值范围是
 
．
已知函数f（x）=
x+3
，g（x）=3-x，构造函数y=F（x），定义如下：当f（x）≥g（x）时，F（x）=g（x）；当f（x）＜g（x）时，F（x）=f（x），则F（x）的最大值为
 
．
已知圆C的极坐标方程为ρ=2cosθ，直线l的参数方程为
x=5-
3
t
y=t
（t为参数），设A，B分别为圆C和直线l上的动点，则|AB|的最小值为
 
．
数列{an}满足a1=a2=1，an+an+1+an+2=cos
2nπ
3
（n∈N*），若数列{an}的前n项和为Sn，则S20的值为（　　）
A、-4B、-1C、8D、5
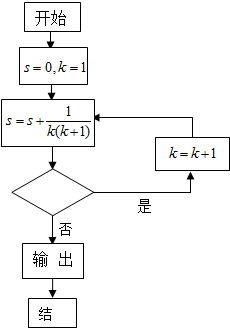
若如图所示的框图所给程序运行的结果S=
2010
2011
，那么判断框中可以填入的关于实数k的判断条件应是（　　）
A、k＜2010
B、k＜2009
C、k＞2010
D、k＞2009
若抛物线y2=ax经过不等式组
x-y-2≥0
x+2y-8≤0
y≥1
表示的平面区域，则抛物线焦点的横坐标的取值范围是（　　）
A、[
1
24
，
1
4
]
B、[
1
12
，
1
2
]
C、[
1
6
，1]
D、[
1
4
，
3
2
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网