题目内容
已知定点Q(2,-1),F为抛物线y2=4x的焦点,动点P为抛物线上任意一点,当|PQ|+|PF|取最小值时P的坐标为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:作PM⊥准线x=-1,交准线于M点,由抛物线定义和两点间线段最短,知:当M,P,Q三点线时,|PQ|+|PF|=|PQ|+|PM|取最小值,由此能求出结果.
解答:
解:如图,作PM⊥准线x=-1,交准线于M点,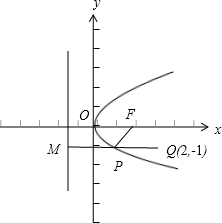
由抛物线定义知:|PF|=|PM|,
∴|PQ|+|PF|=|PQ|+|PM|,
∵点Q(2,-1)在抛物线y2=4x内部,
∴由两点间线段最短,知:当M,P,Q三点线时,
∴|PQ|+|PF|=|PQ|+|PM|取最小值,
此时点P的纵坐标y=-1,
把y=-1代入y2=4x,解得x=
,
∴当|PQ|+|PF|取最小值时P的坐标为(
,-1).
故答案为:(
,-1).

由抛物线定义知:|PF|=|PM|,
∴|PQ|+|PF|=|PQ|+|PM|,
∵点Q(2,-1)在抛物线y2=4x内部,
∴由两点间线段最短,知:当M,P,Q三点线时,
∴|PQ|+|PF|=|PQ|+|PM|取最小值,
此时点P的纵坐标y=-1,
把y=-1代入y2=4x,解得x=
| 1 |
| 4 |
∴当|PQ|+|PF|取最小值时P的坐标为(
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题考查两条线段和取最小值对应点的坐标的求法,是中档题,解题时要熟练掌握抛物线的简单性质,注意数形结合思想的合理运用.

练习册系列答案
相关题目
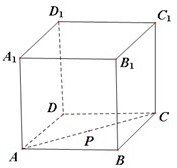 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题: