题目内容
5．设复数$z=\frac{{2{i^3}}}{i-1}$（i为虚数单位），z则的虚部为（ ）| A． | i | B． | -i | C． | -1 | D． | 1 |
分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：∵$z=\frac{{2{i^3}}}{i-1}$=$\frac{-2i}{（-1+i）}=\frac{-2i（-1-i）}{（-1+i）（-1-i）}=\frac{-2+2i}{2}=-1+i$，
∴z的虚部为1．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
16．已知焦点在x轴上的椭圆的离心率为$\frac{1}{2}$，且它的长轴长等于4，则椭圆的标准方程是（ ）
| A． | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | B． | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C． | $\frac{x^2}{4}+{y^2}=1$ | D． | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
10．已知α为第二象限角，sin（π+α）=-$\frac{1}{3}$，则tanα=（ ）
| A． | -$\frac{\sqrt{2}}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
17．
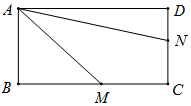如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）
如图，某地区有四个公司分别位于矩形ABCD的四个顶点，且AB=1km，BC=2km，四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草，其中M，N分别在直线BC，CD上运动，∠MAN=30°，设∠BAM=α，当三角AMN的面积最小时，此时α=（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{5π}{12}$ |
14．已知函数$f（x）=\sqrt{x}sinx$，则f'（π）=（ ）
| A． | $\sqrt{π}$ | B． | $\frac{{\sqrt{π}}}{2π}$ | C． | $-\sqrt{π}$ | D． | $\frac{{\sqrt{2π}}}{2π}$ |