题目内容
11.已知f(x)=x+alnx(a>0)对于区间[1,3]内的任意两个相异实数x1,x2,恒有$|f({x_1})-f({x_2})|<|\frac{1}{x_1}-\frac{1}{x_2}|$成立,则实数a的取值范围是(0,$\frac{8}{3}$).分析 问题等价于|1+$\frac{a(l{nx}_{1}-l{nx}_{2})}{{{x}_{1}-x}_{2}}$|<$\frac{1}{{{|x}_{1}x}_{2}|}$,(1),由x1,x2→$\frac{1}{3}$时(1)变为|1+3a|<9,由x1,x2→1时(1)变为|1+a|<1,得到关于a的不等式,解出即可.
解答 解:已知a>0,f(x)=x+alnx,
对区间[1,3]内的任意两个相异的实数x1,x2,恒有|f(x1)-f(x2)|<|$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$|,
∴|x1-x2+a(lnx1-lnx2)|<|$\frac{{{x}_{1}-x}_{2}}{{{x}_{1}x}_{2}}$|,
两边都除以|x1-x2|,
∵|1+$\frac{a(l{nx}_{1}-l{nx}_{2})}{{{x}_{1}-x}_{2}}$|<$\frac{1}{{{|x}_{1}x}_{2}|}$,(1)
(lnx)′=$\frac{1}{x}$∈[$\frac{1}{3}$,1],
∴$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$∈[$\frac{1}{3}$,1],
x1,x2→$\frac{1}{3}$时(1)变为|1+3a|<9,
解得:-$\frac{10}{3}$<a<$\frac{8}{3}$,
x1,x2→1时(1)变为|1+a|<1,
解得:-2<a<0,
又∵a>0,
∴0<a<$\frac{8}{3}$,
故答案为(0,$\frac{8}{3}$).
点评 本题考查了求函数闭区间上的最值问题,考查了导数的应用,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知双曲线$C:{x^2}-\frac{y^2}{3}=1$的右顶点为A,过右焦点F的直线l与C的一条渐近线平行,交另一条渐近线于点B,则S△ABF=( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{3}}}{8}$ |
19.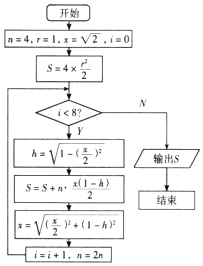 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
 我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.
我国魏晋时期的数学家刘徽,他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π,用刘徽自己的原话就是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体而无所失矣.”设计程序框图是计算圆周率率不足近似值的算法,其中圆的半径为1.请问程序中输出的S是圆的内接正( )边形的面积.| A. | 1024 | B. | 2048 | C. | 3072 | D. | 1536 |
6.已知$\frac{1-ai}{1+i}=b-i$(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |