题目内容
15.已知椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,离心率为$\frac{1}{2}$,点F为其在y轴正半轴上的焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)若一动圆过点F,且与直线y=-1相切,求动圆圆心轨迹C1的方程;
(Ⅲ)过F作互相垂直的两条直线l1,l2,其中l1交曲线C1于M、N两点,l2交椭圆C于P、Q两点,求四边形PMQN面积的最小值.
分析 (I)由题意可得:2b=2$\sqrt{3}$,$\frac{c}{a}=\frac{1}{2}$,又a2=b2+c2,联立解得即可得出.
(II)F(0,1),由题意可得:动圆圆心轨迹为抛物线,点F为焦点,直线y=-1为准线,即可得出方程.
(III)由题意可设直线l1的方程为:y=kx+1,(k≠0),M(x1,y1),N(x2,y2).
则直线l1的方程为:y=-$\frac{1}{k}$x+1,P(x3,y3),Q(x4,y4).与抛物线方程联立可得:x2-4kx-4=0,利用根与系数的关系代入|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=4(1+k2).同理可得|PQ|=4$(1+\frac{1}{{k}^{2}})$,利用S四边形PMQN=$\frac{1}{2}$|MN|•|PQ|,及其基本不等式的性质即可得出.
解答 解:(I)由题意可得:2b=2$\sqrt{3}$,$\frac{c}{a}=\frac{1}{2}$,又a2=b2+c2,
联立解得b=$\sqrt{3}$,a=2,c=1.
∴椭圆C的方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}$=1.
(II)F(0,1),由题意可得:动圆圆心轨迹为抛物线,点F为焦点,直线y=-1为准线,
因此C1的方程为:x2=4y.
(III)解:由题意可设直线l1的方程为:y=kx+1,(k≠0),M(x1,y1),N(x2,y2).
则直线l1的方程为:y=-$\frac{1}{k}$x+1,P(x3,y3),Q(x4,y4).
联立$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$,可得:x2-4kx-4=0,可得x1+x2=4k,x1•x2=-4,
∴|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=4(1+k2).
同理可得|PQ|=4$(1+\frac{1}{{k}^{2}})$,
∴S四边形PMQN=$\frac{1}{2}$|MN|•|PQ|=8(1+k2)$(1+\frac{1}{{k}^{2}})$=8$(2+{k}^{2}+\frac{1}{{k}^{2}})$≥8$(2+2\sqrt{{k}^{2}•\frac{1}{{k}^{2}}})$=32,
当且仅当k=±1时取等号,此时四边形PMQN面积的最小值为32.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、基本不等式的性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案(1)求a,b的值;
(2)设x≥0,求证:f(x)>x2+4x-14.
| A. | {x|x≤3} | B. | {x|2<x<3} | C. | {x|-1≤x≤3} | D. | R |
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | $\frac{7}{2}$ | B. | 7 | C. | -1或7 | D. | -$\frac{1}{2}$或$\frac{7}{2}$ |
| A. | 不含x9项 | B. | 含x4项 | C. | 含x2项 | D. | 不含x项 |
| A. | $\frac{1}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
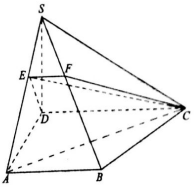 如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.
如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.