题目内容
6.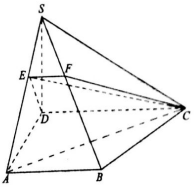 如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.
如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.(1)求证:EF∥CD;
(2)求三棱锥S-DEF的体积.
分析 (1)由CD∥AB,知CD∥平面SAB,由此能证明CD∥EF.
(2)推导出EF⊥平面SAD,由此能求出三棱锥S-DEF的体积.
解答 证明:(1)∵在直角梯形ABCD中CD∥AB,
AB?平面SAB,CD?平面SAB,
∴CD∥平面SAB,
又∵平面CDEF∩平面SAB=EF,
∴CD∥EF.…(6分)
解:(2)∵CD⊥AD,平面SAD⊥平面ABCD,
∴CD⊥平面SAD,∴CD⊥SD,同理AD⊥SD,
由(1)知EF∥CD,∴EF⊥平面SAD,
∵EC=AC,∠ADC=∠EDC=90°,
∴△ADC≌△EDC,∴ED=AD,
在Rt△SDA中,∵AD=1,SD=$\sqrt{3}$,∠SAD=60°,
又∵ED=AD=1,∴E为SA中点,EF=$\frac{1}{2}AB$=$\frac{1}{2}$,
∴△SED的面积为$\frac{\sqrt{3}}{4}$,
∴三棱锥S-DEF的体积V=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{1}{2}=\frac{\sqrt{3}}{24}$.…(12分)
点评 本题考查线线平行的证明,考查三棱锥的体积的求法,是中档题,解题时要 认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设集合M={x|x2-x-2<0},N={x|x≤k},若M∩N=M,则k的取值范围是( )
| A. | (-∞,2] | B. | [-1,+∞) | C. | (-1,+∞) | D. | [2,+∞) |
11.函数y=cos$\frac{x}{2}$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
 将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.
将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.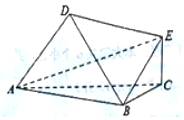 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.