题目内容
5.设复数z1=1-i,z2=1+i,其中i是虚数单位,则$\frac{{z}_{1}}{{z}_{2}}$的模为( )| A. | $\frac{1}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 直接把z1,z2代入$\frac{{z}_{1}}{{z}_{2}}$,再利用复数代数形式的乘除运算化简,根据复数求模公式计算即可得答案.
解答 解:由z1=1-i,z2=1+i,
得$\frac{{z}_{1}}{{z}_{2}}$=$\frac{1-i}{1+i}=\frac{(1-i)^{2}}{(1+i)(1-i)}=\frac{-2i}{2}=-i$,
则$\frac{{z}_{1}}{{z}_{2}}$的模为:1.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
20. 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
(1)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取3名学生,记“获奖”学生人数为X,求X的分布列及数学期望.
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).(1)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取3名学生,记“获奖”学生人数为X,求X的分布列及数学期望.
| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.函数y=$\sqrt{x}$lg(3-x)的定义域为( )
| A. | (0,3) | B. | [0,3) | C. | (0,3] | D. | [0,3] |
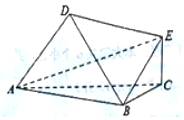 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2. 如图,给定由10个点(任意相邻两点距离为1,)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )
如图,给定由10个点(任意相邻两点距离为1,)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )