题目内容
17.F1、F2是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{7}$=1的两个焦点,A为椭圆上一点,且∠F1AF2=60°,则△F1AF2的面积为$\frac{7\sqrt{3}}{3}$.分析 利用椭圆的定义,可求得|AF1|+|AF2|=2a=6,|F1F2|=2c=2$\sqrt{2}$,先由余弦定理求得|AF1|•|AF2|=$\frac{28}{3}$,再利用正弦定理即可求得△F1AF2的面积S=$\frac{1}{2}$|AF1|•|AF2|sin∠F1AF2.
解答  解:依题意,作图如下:
解:依题意,作图如下:
∵a2=9,b2=7,
∴c2=a2-b2=2,
又|AF1|+|AF2|=2a=6,|F1F2|=2c=2$\sqrt{2}$,∠F1AF2=60°,
在△F1AF2中,由余弦定理得:
|F1F2|2=|AF1|2+|AF2|2-2|AF1|•|AF2|cos∠F1AF2
=(|AF1|+|AF2|)2-3|AF1|•|AF2|,
即4c2=4a2-3|AF1|•|AF2|,
∴3|AF1|•|AF2|=4b2=28,
∴|AF1|•|AF2|=$\frac{28}{3}$,
∴△F1AF2的面积S=$\frac{1}{2}$|AF1|•|AF2|sin∠F1AF2=$\frac{1}{2}$×$\frac{28}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{{7\sqrt{3}}}{3}$.
故答案为:$\frac{7\sqrt{3}}{3}$.
点评 本题考查椭圆的简单性质,着重考查椭圆的定义与a、b、c之间的关系式的应用,考查三角形的面积公式,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
8.某工厂去年产值为a,计划从今年起的今后10年内每年比上年产值增加10%,则这个厂第5年的产值为( )
| A. | 1.5a | B. | 1.15a | C. | 1.14a | D. | 11×(1.15-1)a |
12.函数f(x)=x2-3|x|-k有两个零点,则k的取值范围是( )
| A. | (0,+∞)$∪\{-\frac{9}{4}\}$ | B. | $[-\frac{9}{4},+∞)$ | C. | [0,+∞) | D. | $(-∞,-\frac{9}{4})∪\{0\}$ |
9.三个数$a={0.5^{1.5}},b={log_2}0.5,c={2^{0.3}}$之间的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
6.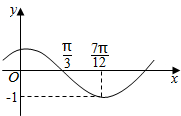 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |