题目内容
6.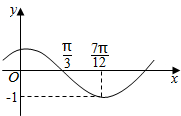 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数的解析式,利用诱导公式可得f(x)=cos2(x-$\frac{π}{12}$),再根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由函数的图象可得 A=1,由 $\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,可得ω=2.
再根据五点法作图可得 2×$\frac{π}{3}$+φ=π 求得 φ=$\frac{π}{3}$,
故函数的解析式为 f(x)=sin(2x+$\frac{π}{3}$).
由f(x)=sin(2x+$\frac{π}{3}$)=cos($\frac{π}{6}$-2x)=cos2(x-$\frac{π}{12}$),
故将f(x)的图象向左平移$\frac{π}{12}$个单位,即可得到g(x)=cos2x的图象.
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,诱导公式,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.

练习册系列答案
相关题目
16.已知全集U=R,集合$A=\{x|y=\sqrt{\frac{4-x}{x-2}}\},B=\{x|{x^2}-7x+12≤0\},则A∩$(∁UB)=( )
| A. | (2,3) | B. | (2,4) | C. | (3,4] | D. | (2,4] |
14.一个正六棱锥体积为$2\sqrt{3}$,底面边长为2,则其侧面积为( )
| A. | 12 | B. | 6 | C. | 18 | D. | 10 |
15.若幂函数y=(m2-3m+3)xm-2的图象不过原点,则( )
| A. | 1≤m≤2 | B. | m=1或m=2 | C. | m=2 | D. | m=1 |