题目内容
已知点A（1，-2，0）和
=（-3，4，12），求点B的坐标，使
∥
，且|AB|等于|
|的2倍．
| a |
| AB |
| a |
| a |
考点：空间向量的夹角与距离求解公式,共线向量与共面向量
专题：空间向量及应用
分析：设
=n
=（-3n，4n，12n），由|
|=2|
|，得n=2或n=-2，由此利用
=
+
，能求出点B的坐标．
| AB |
| a |
| AB |
| a |
| OB |
| OA |
| AB |
解答：
解：∵
∥
，∴可设
=n
=（-3n，4n，12n），
∵|
|=13，∴|
|=|n|•|
|=13|n|
∵|
|=2|
|，13|n|=26，解得n=2或n=-2，
当n=2时，
=
+
=（1，-2，0）+（-6，8，24）=（-5，6，24），
当n=-2时，
=
+
=（1，-2，0）+（6，-8，-24）=（7，-10，-24），
故B为（-5，6，24）或（7，-10，-24）．
| AB |
| a |
| AB |
| a |
∵|
| a |
| AB |
| a |
∵|
| AB |
| a |
当n=2时，
| OB |
| OA |
| AB |
当n=-2时，
| OB |
| OA |
| AB |
故B为（-5，6，24）或（7，-10，-24）．
点评：本题考查点的坐标的求法，是基础题，解题时要认真审题，注意空间向量的坐标运算法则的合理运用．
练习册系列答案
相关题目
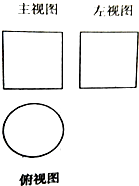如图一个空间几何体的主视图和左视图都是边长为2的正方形，俯视图是一个圆，则该几何体的侧面积为
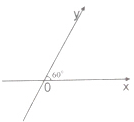如图所示，∠xoy=60°，