题目内容
椭圆C的焦点分别为F1(-1,0)F2(1,0),P(1,
)是椭圆上的一个点
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设原点为O,斜率为
的直线l过点F1且与椭圆C相交于A、B两点,求△AOB的面积.
| ||
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设原点为O,斜率为
| ||
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(I)由题意可设椭圆的标准方程为
+
=1(a>b>0),可得c=1,
+
=1,a2=b2+c2,解出即可.
(Ⅱ)设点A(x1,y1),B(x2,y2).依题意得直线l的方程为:y=
(x+1),与椭圆方程联立可得根与系数的关系,利用弦长公式|AB|=
.
点到直线的距离公式可得原点O到直线l的距离d.再利用S△AOB=
d•|AB|即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| 2b2 |
(Ⅱ)设点A(x1,y1),B(x2,y2).依题意得直线l的方程为:y=
| ||
| 2 |
(1+
|
点到直线的距离公式可得原点O到直线l的距离d.再利用S△AOB=
| 1 |
| 2 |
解答:
解:(I)由题意可设椭圆的标准方程为
+
=1(a>b>0),c为半焦距.
可知:c=1,
+
=1,a2=b2+c2,
联立解得b2=1,c=1,a2=2.
∴椭圆C的标准方程为
+y2=1.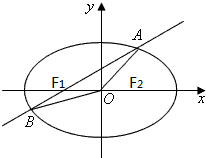
(Ⅱ)设点A(x1,y1),B(x2,y2).
依题意得直线l的方程为:y=
(x+1),
联立
,化为2x2+2x-1=0,
∴x1+x2=-1,x1x2=-
.
∴|AB|=
=
=
.
原点O到直线l的距离为:d=
=
.
∴S△AOB=
d•|AB|=
×
×
=
.
| x2 |
| a2 |
| y2 |
| b2 |
可知:c=1,
| 1 |
| a2 |
| 1 |
| 2b2 |
联立解得b2=1,c=1,a2=2.
∴椭圆C的标准方程为
| x2 |
| 2 |

(Ⅱ)设点A(x1,y1),B(x2,y2).
依题意得直线l的方程为:y=
| ||
| 2 |
联立
|
∴x1+x2=-1,x1x2=-
| 1 |
| 2 |
∴|AB|=
(1+
|
|
3
| ||
| 2 |
原点O到直线l的距离为:d=
|
| ||||
|
| ||
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
3
| ||
| 2 |
| ||
| 4 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
若(a-3)-3<(1+2a)-3,则实数a的取值范围是( )
| A、(-4,+∞) | ||
B、{a|a>-4,a≠3且a≠-
| ||
| C、(-∞,-4) | ||
D、(-∞,-4)∪(-
|
 已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,
已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,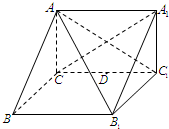 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.