题目内容
已知P是抛物线y2=2x上的一个动点，过P作圆（x-3）2+y2=1的切线，切点分别为M、N，则|MN|的最小值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：利用导数研究曲线上某点切线方程
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：根据题意，利用等面积可得|MN|=2|ME|=
=
=
=2
，所以当|PO1|最小时，|MN|取最小值，故可求．
| 2|PM||O1M| |
| |PO1| |
| 2|PM| |
| |PO1| |
2
| ||
| |PO1| |
1-
|
解答：
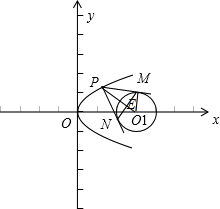解：设圆心为O1（3，0），PO1与MN交于E，
则|PO1|2=|PM|2+1，
由等面积可知：|MN|=2|ME|=
=
=
=2
，
则当|PO1|最小时，|MN|取最小值，|PO1|=
=
=
，
则当x=2时，|PO1|有最小值
，
故|MN|最小值是|MN|═2
=
．
故选C．
解：设圆心为O1（3，0），PO1与MN交于E，则|PO1|2=|PM|2+1，
由等面积可知：|MN|=2|ME|=
| 2|PM||O1M| |
| |PO1| |
| 2|PM| |
| |PO1| |
=
2
| ||
| |PO1| |
1-
|
则当|PO1|最小时，|MN|取最小值，|PO1|=
| (x-3)2+y2 |
=
| (x-3)2+2x |
| (x-2)2+5 |
则当x=2时，|PO1|有最小值
| 5 |
故|MN|最小值是|MN|═2
1-
|
4
| ||
| 5 |
故选C．
点评：本题重点考查圆与抛物线的综合，考查距离最小值的求解，解题的关键是利用等面积可得|MN|=2|ME|=2
，考查化简运算能力，属于中档题．
1-
|
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
设I为全集，集合M，N，P都是其子集，则图中的阴影部分表示的集合为（ ）
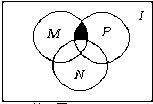
| A、M∩（N∪P） |
| B、M∩（P∩∁IN） |
| C、P∩（∁IN∩∁IM ） |
| D、（M∩N）∪（M∩P） |
设Sn为等差数列{an}的前n项和，（n+1）Sn＜nSn+1（n∈N*）．若
＜-1，则（ ）
| a8 |
| a7 |
| A、Sn的最大值为S8 |
| B、Sn的最小值为S8 |
| C、Sn的最大值为S7 |
| D、Sn的最小值为S7 |
在等比数列{an}中，a1=
，a4=
，则数列的公比q为（ ）
| 1 |
| 2 |
| 1 |
| 16 |
A、
| ||
B、±
| ||
C、
| ||
D、±
|
下列命题中，真命题是（ ）
| A、?x0∈R，e x0≤0 | ||
| B、?x∈R，2x＞x2 | ||
C、a+b=0的充要条件是
| ||
| D、a＞1且b＞1是ab＞1的充分条件 |