题目内容
6．在△ABC中，已知b=2a，B=30°，则cosA=$\frac{{\sqrt{15}}}{4}$．分析 由已知及正弦定理可求sinA=$\frac{1}{4}$，且A为锐角，利用同角三角函数基本关系式即可求值cosA的值．
解答 解：∵b=2a，B=30°，
∴sinB=2sinA=$\frac{1}{2}$，可得sinA=$\frac{1}{4}$，且A为锐角，
∴cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{{\sqrt{15}}}{4}$．
故答案为：$\frac{{\sqrt{15}}}{4}$．
点评 本题主要考查了正弦定理，同角三角函数基本关系式在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
16．各项均为正数的等差数列{an}中，前n项和为Sn，当n∈N*，n≥2时，有${S_n}=\frac{n}{n-1}（{a_n}^2-{a_1}^2）$，则S20-2S10=（ ）
| A． | 50 | B． | -50 | C． | 100 | D． | -100 |
1．已知数列{an}的前n项和为Sn，若an+1=an-1，a1=4，则S6等于（ ）
| A． | 25 | B． | 20 | C． | 15 | D． | 9 |
11．设z=1-i（为虚数单位），则${z^2}+\frac{2}{z}$=（ ）
| A． | 1-i | B． | -1+i | C． | -1-i | D． | 1+i |
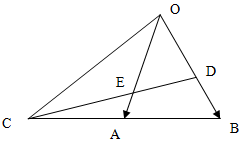已知△ABO中，延长BA到C，使AC=BA，D是将$\overrightarrow{OB}$分成2：1的一个分点，DC和OA交于E，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$
15．设集合M={-2，2}，N={x|$\frac{1}{x}$＜2}，则下列结论正确的是（ ）
| A． | N⊆M | B． | M⊆N | C． | N∩M={2} | D． | N∪M=R |