题目内容
10.已知函数f(x)=$\frac{a}{3}{x^3}$+$\frac{1}{2}$(1-a2)x2-ax,其中a∈R.(1)若曲线y=f(x)在点(1,f(1))处的切线方程为8x+y-2=0,求a的值;
(2)当a≠0时,求函数f(x)(x>0)的单调区间与极值;
(3)若a=1,存在实数m,使得方程f(x)=m恰好有三个不同的解,求实数m的取值范围.
分析 (1)求导,由f'(1)=-8,求得a的值,分别求得切线方程,与原切线方程比较,即可求得a的值;
(2)求导,根据导数与函数单调性的关系,分类讨论,即可求得函数f(x)(x>0)的单调区间与极值;
(3)由(2)可知:根据函数的单调性,求得f(x)的极值,分别作出函数$f(x)=\frac{1}{3}{x^3}-x$与y=m的图象,从图象上可以看出当$-\frac{2}{3}<m<\frac{2}{3}$时,两个函数的图象有三个不同的交点,即可求得m的取值范围.
解答 解:(1)f'(x)=ax2+(1-a2)x-a,由8x+y-2=0可得f'(1)=-8,
即f'(1)=a+(1-a2)-a=-8,解得a=±3,
当a=3时,f(x)=x3-4x2-3x,f(1)=-6,f'(x)=3x2-8x-3,f'(1)=-8,
当a=-3时,f(x)=-x3-4x2+3,f(1)=-2,f'(x)=-3x2-8x+3,f'(1)=-8,
故曲线y=f(x)在点(1,f(1))处的切线方程为y+2=-8(x-1),即8x+y-6=0不符合题意,舍去,
故a的值为3.
(2)当a≠0时,f′(x)=ax2+(1-a2)x-a=(x-a)(ax+1)=a(x-a)(x+$\frac{1}{a}$),
当a>0时,令f'(x)=0,则${x_1}=-\frac{1}{a},{x_2}=a$
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,a) | a | (a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
函数f(x)在${x_1}=-\frac{1}{a}$处取得最大值$f(-\frac{1}{a})$,且$f(-\frac{1}{a})=\frac{a}{3}×{(-\frac{1}{a})^3}+\frac{1}{2}(1-{a^2})×{(-\frac{1}{a})^2}+1=\frac{1}{{6{a^2}}}+\frac{1}{2}$.
函数f(x)在x2=a处取得极小值f(a),且$f(a)=\frac{a}{3}×{a^3}+\frac{1}{2}(1-{a^2})×{a^2}-a×a=-\frac{1}{6}{a^4}-\frac{1}{2}{a^2}$,
当a<0时,令f'(x)=0,则${x_1}=a,{x_2}=-\frac{1}{a}$,
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,a) | a | (a,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ |
函数f(x)在${x_1}=-\frac{1}{a}$处取得极大值$f(-\frac{1}{a})$,
且$f(-\frac{1}{a})=\frac{a}{3}{(-\frac{1}{a})^3}+\frac{1}{2}(1-{a^2})•{(-\frac{1}{a})^2}-a×(-\frac{1}{a})=\frac{1}{{6{a^2}}}+\frac{1}{2}$.
函数f(x)在x2=a处取得极小值f(a),且$f(a)=\frac{a}{3}×{a^3}+\frac{1}{2}(1-{a^2})×{a^2}-a×a=-\frac{1}{6}{a^4}-\frac{1}{2}{a^2}$,
(3)若a=1,则$f(x)=\frac{1}{3}{x^3}-x,f'(x)={x^2}-1$,
由(2)可知$f(x)=\frac{1}{3}{x^3}-x$在区间(-∞,-1),(1,+∞)内增函数,在区间(-1,1)内为减函数,
函数f(x)在x1=1处取的极小值f(1),且$f(1)=-\frac{1}{6}-\frac{1}{2}=-\frac{2}{3}$.
函数f(x)在x2=-1处取得极大值f(-1),且$f({-1})=\frac{1}{6}\frac{1}{2}=\frac{2}{3}$.
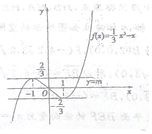
如图分别作出函数$f(x)=\frac{1}{3}{x^3}-x$与y=m的图象,
从图象上可以看出当$-\frac{2}{3}<m<\frac{2}{3}$时,两个函数的图象有三个不同的交点,
即方程f(x)=m有三个不同的解,
故实数m的取值范围为$(-\frac{2}{3},\frac{2}{3})$.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性区间及最值,考查方程解得个数,考查数形结合思想,考查计算能力,属于难题.

练习册系列答案
相关题目
1.已知数列{an}的前n项和为Sn,若an+1=an-1,a1=4,则S6等于( )
| A. | 25 | B. | 20 | C. | 15 | D. | 9 |
15.设集合M={-2,2},N={x|$\frac{1}{x}$<2},则下列结论正确的是( )
| A. | N⊆M | B. | M⊆N | C. | N∩M={2} | D. | N∪M=R |
19.已知函数y=f(x)+x3是R上的偶函数,若f(1)=2,则f(-1)=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
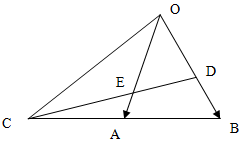 已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$