题目内容
三棱锥的三个侧面与底面所成的二面角都相等，那么这个三棱锥顶点在底面三角形所在平面上射影O必是底面三角形的（ ）
| A、内心 | B、外心 | C、垂心 | D、重心 |
考点：二面角的平面角及求法
专题：计算题,空间位置关系与距离
分析：顶点在底面上的射影，以及二面角，构成的三个三角形是全等三角形，推出垂足到三边距离相等，可得结果．
解答：
解：侧面与底面所成的二面角都相等，
并且顶点在底面的射影在底面三角形内则底面三条高的垂足、
三棱锥的顶点和顶点在底面的射影这三者构成的3个三角形是全等三角形，
所以顶点在底面的射影到底面三边的距离相等，
所以是内心．
故选A
并且顶点在底面的射影在底面三角形内则底面三条高的垂足、
三棱锥的顶点和顶点在底面的射影这三者构成的3个三角形是全等三角形，
所以顶点在底面的射影到底面三边的距离相等，
所以是内心．
故选A
点评：本题考查棱锥的结构特征，考查二面角，考查逻辑思维能力，是中档题．
练习册系列答案
相关题目
函数y=5sin6x是（ ）
A、周期是
| ||
| B、周期是3π的偶函数 | ||
C、周期是
| ||
D、周期是
|
双曲线
-y2=1的右焦点到直线x-
y=0的距离是（ ）
| x2 |
| 3 |
| 3 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
若m，n是两条不同的直线，α，β，γ为三个不同的平面，则下列命题正确的是（ ）
| A、若m∥n，m?α，则n∥α |
| B、若m∥n，m?α，n?β，则β∥α |
| C、若α⊥γ，β⊥α，则β∥γ |
| D、若m∥n，m⊥α，n⊥β，则β∥α |
已知点F1，F2分别是双曲线C：
-
=1（a＞0，b＞0）的左、右焦点，过F2且垂直于x轴的直线与C交于A，B两点，若△ABF1为等腰直角三角形，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
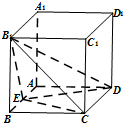如图，正方体ABCD-A1B1C1D1中，E是AB的中点