题目内容
已知双曲线
-
=1(a>0,b>0)的渐近线与抛物线x2=2y在点(2,2)处的切线平行,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先利用导数求出切线的斜率,再根据双曲线
-
=1(a>0,b>0)的渐近线与抛物线x2=2y在点(2,2)处的切线平行求出渐近线的斜率,最后根据离心率公式求出所求即可.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:∵x2=2y,∴y=
x2,∴y′=x则y′|x=2=2
∴抛物线x2=2y在点(2,2)处的切线斜率为2,
∵双曲线
-
=1(a>0,b>0)的渐近线与抛物线x2=2y在点(2,2)处的切线平行,
∴
=2,
∴e=
=
=
.
故选:A.
| 1 |
| 2 |
∴抛物线x2=2y在点(2,2)处的切线斜率为2,
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴
| b |
| a |
∴e=
| c |
| a |
1+(
|
| 5 |
故选:A.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及双曲线的简单性质,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
若双曲线x2+
=1的离心率是2,则焦距为( )
| y2 |
| k |
| A、2 | ||
B、2
| ||
C、2
| ||
| D、4 |
在△ABC中,a=
,b=
,B=
,则A=( )
| 2 |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
三棱锥的三个侧面与底面所成的二面角都相等,那么这个三棱锥顶点在底面三角形所在平面上射影O必是底面三角形的( )
| A、内心 | B、外心 | C、垂心 | D、重心 |


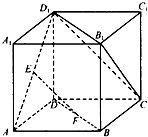 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.