题目内容
15.已知各项均为正数的数列{an}的前n项和Sn满足8Sn=a${\;}_{n}^{2}$+4an+3(∈N*).(1)求数列{an}的通项公式;
(2)设bn=$\frac{n}{(2n+1){S}_{n}}$,是否存在一个最小的常数M,使得b1+b2+…+bn<m对于任意的n∈N*均成立,若存在,求出常数m;若不存在,请说明理由.
分析 (I)利用递推关系与等差数列的通项公式即可得出;
(II)利用等差数列的前n项和公式、“裂项求和”即可得出.
解答 解:(Ⅰ)∵$8{S_n}={a_n}^2+4{a_n}+3$,
∴8Sn-1=${a}_{n-1}^{2}$+4an-1+3,(n≥2),
∴$8({S_n}-{S_{n-1}})={a_n}^2+4{a_n}-{a^2}_{n-1}-4{a_{n-1}}$,
∴${a_n}^2-{a^2}_{n-1}=4({a_n}+{a_{n-1}})$
∵an>0,∴an-an-1=4(n≥2),
∴数列{an}是以4为公差的等差数列.
又∵$8{S_1}={a_1}^2+4{a_1}+3$,
∴${a_1}^2-4{a_1}+3=0$,而a1<3,
∴a1=1.
∴an=4n-3(n∈N*).
(Ⅱ)由(Ⅰ)知${S_n}=n•1+\frac{n(n-1)}{2}•4=2{n^2}-n$,
∴${b_n}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${b_1}+{b_2}+…+{b_n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})=\frac{n}{2n+1}$,
∵$\frac{n}{2n+1}=\frac{1}{{2+\frac{1}{n}}}<\frac{1}{2}$,
∴存在$m≥\frac{1}{2}$,使b1+b2+…+bn<m对于任意的正整数n均成立.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”、递推关系、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{4}{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
| A. | ?x0∈R,使得x0+$\frac{1}{x0}$=$\frac{3}{2}$ | B. | ?x∈(0,+∞),ex>x+1 | ||
| C. | ?x0∈R,使得x${\;}_{{0}^{\;}}$2-x0+1=0 | D. | ?x∈(0,π),sinx>cosx |
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 垂直于同一平面的两条直线互相平行 | |
| C. | 垂直于同一平面的两个平面互相平行 | |
| D. | 平行于同一平面的两条直线互相平行 |

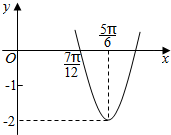 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1.