题目内容
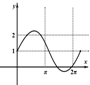
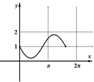
3.某几何体的三视图如图所示,则该几何体的体积为$\frac{16}{3}$.
分析 由三视圆得该几何体由直三棱柱ABC-A1B1C1与三棱锥B-B1C1D组合而成,其中A1B1DC1是边长为2的正方形,AA1=2,由此能求出该几何体的体积.
解答  解:如图,由三视圆得该几何体由直三棱柱ABC-A1B1C1与三棱锥B-B1C1D组合而成,
解:如图,由三视圆得该几何体由直三棱柱ABC-A1B1C1与三棱锥B-B1C1D组合而成,
其中A1B1DC1是边长为2的正方形,AA1=2,
∴该几何体的体积为:
V=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}+{V}_{B-{B}_{1}{C}_{1}D}$
=${S}_{△ABC}•A{A}_{1}+\frac{1}{3}{S}_{△{B}_{1}{C}_{1}D}•A{A}_{1}$
=$\frac{1}{2}×2×2×2+\frac{1}{3}×\frac{1}{2}×2×2×2$
=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查几何体的体积的求法,是基础题,解题时要认真审题,注意三视图的性质的合理运用.

练习册系列答案
相关题目
18.若直线ax+by=2与圆x2+y2=1有公共点,则( )
| A. | a2+b2≤4 | B. | a2+b2≥4 | C. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≤4 | D. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥4 |
8.在△ABC中,角A,B,C的对边分别为a,b,c,若$\frac{2a-c}{b}$=$\frac{cosC}{cosB}$,b=4,则△ABC的面积的最大值为( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
13.下列函数为奇函数的是( )
| A. | y=x2sinx | B. | y=x2cosx | C. | y=|lnx| | D. | y=2-x |